Welcome to Subscribe On Youtube

3157. Find the Level of Tree with Minimum Sum 🔒

Description

Given the root of a binary tree root where each node has a value, return the level of the tree that has the minimum sum of values among all the levels (in case of a tie, return the lowest level).

Note that the root of the tree is at level 1 and the level of any other node is its distance from the root + 1.

 

Example 1:

Input: root = [50,6,2,30,80,7]

Output: 2

Explanation:

Example 2:

Input: root = [36,17,10,null,null,24]

Output: 3

Explanation:

Example 3:

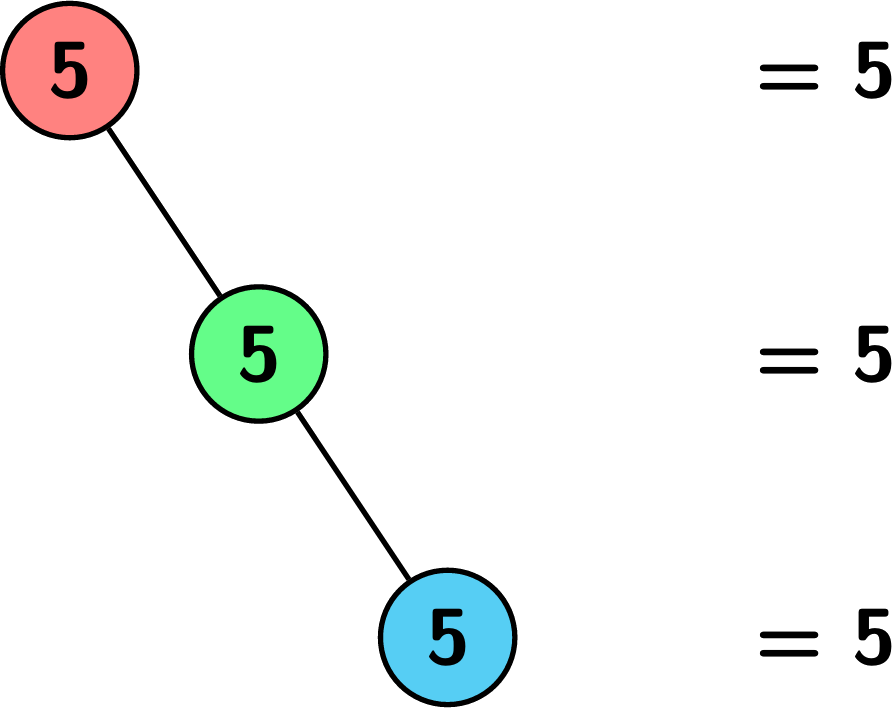
Input: root = [5,null,5,null,5]

Output: 1

Explanation:

 

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 1 <= Node.val <= 109

Solutions

Solution 1: BFS

We can use Breadth-First Search (BFS) to traverse the binary tree level by level, record the sum of the node values at each level, and find the level with the smallest sum of node values, then return the level number.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Where $n$ is the number of nodes in the binary tree.

• Java
• C++
• Python
• Go
• TypeScript

• /**
   * Definition for a binary tree node.
   * public class TreeNode {
   *     int val;
   *     TreeNode left;
   *     TreeNode right;
   *     TreeNode() {}
   *     TreeNode(int val) { this.val = val; }
   *     TreeNode(int val, TreeNode left, TreeNode right) {
   *         this.val = val;
   *         this.left = left;
   *         this.right = right;
   *     }
   * }
   */
  class Solution {
      public int minimumLevel(TreeNode root) {
          Deque<TreeNode> q = new ArrayDeque<>();
          q.offer(root);
          int ans = 0;
          long s = Long.MAX_VALUE;
          for (int level = 1; !q.isEmpty(); ++level) {
              long t = 0;
              for (int m = q.size(); m > 0; --m) {
                  TreeNode node = q.poll();
                  t += node.val;
                  if (node.left != null) {
                      q.offer(node.left);
                  }
                  if (node.right != null) {
                      q.offer(node.right);
                  }
              }
              if (s > t) {
                  s = t;
                  ans = level;
              }
          }
          return ans;
      }
  }
  

• /**
   * Definition for a binary tree node.
   * struct TreeNode {
   *     int val;
   *     TreeNode *left;
   *     TreeNode *right;
   *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
   *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
   *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
   * };
   */
  class Solution {
  public:
      int minimumLevel(TreeNode* root) {
          queue<TreeNode*> q{ {root} };
          int ans = 0;
          long long s = 1LL << 60;
          for (int level = 1; q.size(); ++level) {
              long long t = 0;
              for (int m = q.size(); m; --m) {
                  TreeNode* node = q.front();
                  q.pop();
                  t += node->val;
                  if (node->left) {
                      q.push(node->left);
                  }
                  if (node->right) {
                      q.push(node->right);
                  }
              }
              if (s > t) {
                  s = t;
                  ans = level;
              }
          }
          return ans;
      }
  };
  

• # Definition for a binary tree node.
  # class TreeNode:
  #     def __init__(self, val=0, left=None, right=None):
  #         self.val = val
  #         self.left = left
  #         self.right = right
  class Solution:
      def minimumLevel(self, root: Optional[TreeNode]) -> int:
          q = deque([root])
          ans = 0
          level, s = 1, inf
          while q:
              t = 0
              for _ in range(len(q)):
                  node = q.popleft()
                  t += node.val
                  if node.left:
                      q.append(node.left)
                  if node.right:
                      q.append(node.right)
              if s > t:
                  s = t
                  ans = level
              level += 1
          return ans
  
  

• /**
   * Definition for a binary tree node.
   * type TreeNode struct {
   *     Val int
   *     Left *TreeNode
   *     Right *TreeNode
   * }
   */
  func minimumLevel(root *TreeNode) (ans int) {
  	q := []*TreeNode{root}
  	s := math.MaxInt64
  	for level := 1; len(q) > 0; level++ {
  		t := 0
  		for m := len(q); m > 0; m-- {
  			node := q[0]
  			q = q[1:]
  			t += node.Val
  			if node.Left != nil {
  				q = append(q, node.Left)
  			}
  			if node.Right != nil {
  				q = append(q, node.Right)
  			}
  		}
  		if s > t {
  			s = t
  			ans = level
  		}
  	}
  	return
  }
  

• /**
   * Definition for a binary tree node.
   * class TreeNode {
   *     val: number
   *     left: TreeNode | null
   *     right: TreeNode | null
   *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
   *         this.val = (val===undefined ? 0 : val)
   *         this.left = (left===undefined ? null : left)
   *         this.right = (right===undefined ? null : right)
   *     }
   * }
   */
  
  function minimumLevel(root: TreeNode | null): number {
      const q: TreeNode[] = [root];
      let s = Infinity;
      let ans = 0;
      for (let level = 1; q.length; ++level) {
          const qq: TreeNode[] = [];
          let t = 0;
          for (const { val, left, right } of q) {
              t += val;
              left && qq.push(left);
              right && qq.push(right);
          }
          if (s > t) {
              s = t;
              ans = level;
          }
          q.splice(0, q.length, ...qq);
      }
      return ans;
  }
  
  

All Problems

All Solutions