Welcome to Subscribe On Youtube
3123. Find Edges in Shortest Paths
Description
You are given an undirected weighted graph of n nodes numbered from 0 to n - 1. The graph consists of m edges represented by a 2D array edges, where edges[i] = [ai, bi, wi] indicates that there is an edge between nodes ai and bi with weight wi.
Consider all the shortest paths from node 0 to node n - 1 in the graph. You need to find a boolean array answer where answer[i] is true if the edge edges[i] is part of at least one shortest path. Otherwise, answer[i] is false.
Return the array answer.
Note that the graph may not be connected.
Example 1:
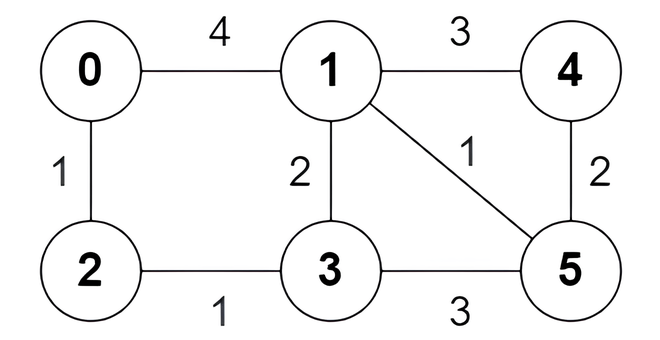
Input: n = 6, edges = [[0,1,4],[0,2,1],[1,3,2],[1,4,3],[1,5,1],[2,3,1],[3,5,3],[4,5,2]]
Output: [true,true,true,false,true,true,true,false]
Explanation:
The following are all the shortest paths between nodes 0 and 5:
- The path
0 -> 1 -> 5: The sum of weights is4 + 1 = 5. - The path
0 -> 2 -> 3 -> 5: The sum of weights is1 + 1 + 3 = 5. - The path
0 -> 2 -> 3 -> 1 -> 5: The sum of weights is1 + 1 + 2 + 1 = 5.
Example 2:
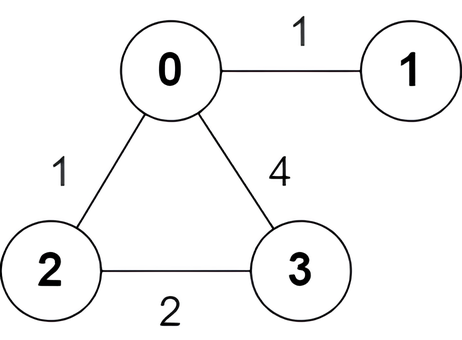
Input: n = 4, edges = [[2,0,1],[0,1,1],[0,3,4],[3,2,2]]
Output: [true,false,false,true]
Explanation:
There is one shortest path between nodes 0 and 3, which is the path 0 -> 2 -> 3 with the sum of weights 1 + 2 = 3.
Constraints:
2 <= n <= 5 * 104m == edges.length1 <= m <= min(5 * 104, n * (n - 1) / 2)0 <= ai, bi < nai != bi1 <= wi <= 105- There are no repeated edges.
Solutions
Solution 1: Heap Optimized Dijkstra
First, we create an adjacency list $g$ to store the edges of the graph. Then we create an array $dist$ to store the shortest distance from node $0$ to other nodes. We initialize $dist[0] = 0$, and the distance of other nodes is initialized to infinity.
Then, we use the Dijkstra algorithm to calculate the shortest distance from node $0$ to other nodes. The specific steps are as follows:
- Create a priority queue $q$ to store the distance and node number of the nodes. Initially, add node $0$ to the queue with a distance of $0$.
- Take a node $a$ from the queue. If the distance $da$ of $a$ is greater than $dist[a]$, it means that $a$ has been updated, so skip it directly.
- Traverse all neighbor nodes $b$ of node $a$. If $dist[b] > dist[a] + w$, update $dist[b] = dist[a] + w$, and add node $b$ to the queue.
- Repeat steps 2 and 3 until the queue is empty.
Next, we create an answer array $ans$ of length $m$, initially all elements are $false$. If $dist[n - 1]$ is infinity, it means that node $0$ cannot reach node $n - 1$, return $ans$ directly. Otherwise, we start from node $n - 1$, traverse all edges, if the edge $(a, b, i)$ satisfies $dist[a] = dist[b] + w$, set $ans[i]$ to $true$, and add node $b$ to the queue.
Finally, return the answer.
The time complexity is $O(m \times \log m)$, and the space complexity is $O(n + m)$, where $n$ and $m$ are the number of nodes and edges respectively.
-
class Solution { public boolean[] findAnswer(int n, int[][] edges) { List<int[]>[] g = new List[n]; Arrays.setAll(g, k -> new ArrayList<>()); int m = edges.length; for (int i = 0; i < m; ++i) { int a = edges[i][0], b = edges[i][1], w = edges[i][2]; g[a].add(new int[] {b, w, i}); g[b].add(new int[] {a, w, i}); } int[] dist = new int[n]; final int inf = 1 << 30; Arrays.fill(dist, inf); dist[0] = 0; PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]); pq.offer(new int[] {0, 0}); while (!pq.isEmpty()) { var p = pq.poll(); int da = p[0], a = p[1]; if (da > dist[a]) { continue; } for (var e : g[a]) { int b = e[0], w = e[1]; if (dist[b] > dist[a] + w) { dist[b] = dist[a] + w; pq.offer(new int[] {dist[b], b}); } } } boolean[] ans = new boolean[m]; if (dist[n - 1] == inf) { return ans; } Deque<Integer> q = new ArrayDeque<>(); q.offer(n - 1); while (!q.isEmpty()) { int a = q.poll(); for (var e : g[a]) { int b = e[0], w = e[1], i = e[2]; if (dist[a] == dist[b] + w) { ans[i] = true; q.offer(b); } } } return ans; } } -
class Solution { public: vector<bool> findAnswer(int n, vector<vector<int>>& edges) { vector<vector<array<int, 3>>> g(n); int m = edges.size(); for (int i = 0; i < m; ++i) { auto e = edges[i]; int a = e[0], b = e[1], w = e[2]; g[a].push_back({b, w, i}); g[b].push_back({a, w, i}); } const int inf = 1 << 30; vector<int> dist(n, inf); dist[0] = 0; using pii = pair<int, int>; priority_queue<pii, vector<pii>, greater<pii>> pq; pq.push({0, 0}); while (!pq.empty()) { auto [da, a] = pq.top(); pq.pop(); if (da > dist[a]) { continue; } for (auto [b, w, _] : g[a]) { if (dist[b] > dist[a] + w) { dist[b] = dist[a] + w; pq.push({dist[b], b}); } } } vector<bool> ans(m); if (dist[n - 1] == inf) { return ans; } queue<int> q{ {n - 1} }; while (!q.empty()) { int a = q.front(); q.pop(); for (auto [b, w, i] : g[a]) { if (dist[a] == dist[b] + w) { ans[i] = true; q.push(b); } } } return ans; } }; -
class Solution: def findAnswer(self, n: int, edges: List[List[int]]) -> List[bool]: g = defaultdict(list) for i, (a, b, w) in enumerate(edges): g[a].append((b, w, i)) g[b].append((a, w, i)) dist = [inf] * n dist[0] = 0 q = [(0, 0)] while q: da, a = heappop(q) if da > dist[a]: continue for b, w, _ in g[a]: if dist[b] > dist[a] + w: dist[b] = dist[a] + w heappush(q, (dist[b], b)) m = len(edges) ans = [False] * m if dist[n - 1] == inf: return ans q = deque([n - 1]) while q: a = q.popleft() for b, w, i in g[a]: if dist[a] == dist[b] + w: ans[i] = True q.append(b) return ans -
func findAnswer(n int, edges [][]int) []bool { g := make([][][3]int, n) for i, e := range edges { a, b, w := e[0], e[1], e[2] g[a] = append(g[a], [3]int{b, w, i}) g[b] = append(g[b], [3]int{a, w, i}) } dist := make([]int, n) const inf int = 1 << 30 for i := range dist { dist[i] = inf } dist[0] = 0 pq := hp{ {0, 0} } for len(pq) > 0 { p := heap.Pop(&pq).(pair) da, a := p.dis, p.u if da > dist[a] { continue } for _, e := range g[a] { b, w := e[0], e[1] if dist[b] > dist[a]+w { dist[b] = dist[a] + w heap.Push(&pq, pair{dist[b], b}) } } } ans := make([]bool, len(edges)) if dist[n-1] == inf { return ans } q := []int{n - 1} for len(q) > 0 { a := q[0] q = q[1:] for _, e := range g[a] { b, w, i := e[0], e[1], e[2] if dist[a] == dist[b]+w { ans[i] = true q = append(q, b) } } } return ans } type pair struct{ dis, u int } type hp []pair func (h hp) Len() int { return len(h) } func (h hp) Less(i, j int) bool { return h[i].dis < h[j].dis } func (h hp) Swap(i, j int) { h[i], h[j] = h[j], h[i] } func (h *hp) Push(v any) { *h = append(*h, v.(pair)) } func (h *hp) Pop() any { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }