Welcome to Subscribe On Youtube
3111. Minimum Rectangles to Cover Points
Description
You are given a 2D integer array points, where points[i] = [xi, yi]. You are also given an integer w. Your task is to cover all the given points with rectangles.
Each rectangle has its lower end at some point (x1, 0) and its upper end at some point (x2, y2), where x1 <= x2, y2 >= 0, and the condition x2 - x1 <= w must be satisfied for each rectangle.
A point is considered covered by a rectangle if it lies within or on the boundary of the rectangle.
Return an integer denoting the minimum number of rectangles needed so that each point is covered by at least one rectangle.
Note: A point may be covered by more than one rectangle.
Example 1:
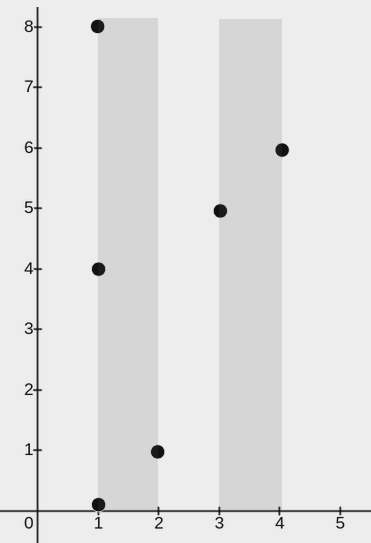
Input: points = [[2,1],[1,0],[1,4],[1,8],[3,5],[4,6]], w = 1
Output: 2
Explanation:
The image above shows one possible placement of rectangles to cover the points:
- A rectangle with a lower end at
(1, 0)and its upper end at(2, 8) - A rectangle with a lower end at
(3, 0)and its upper end at(4, 8)
Example 2:
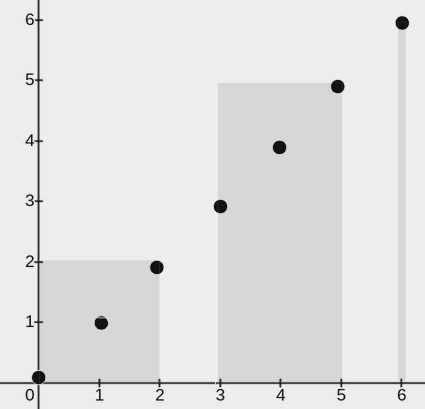
Input: points = [[0,0],[1,1],[2,2],[3,3],[4,4],[5,5],[6,6]], w = 2
Output: 3
Explanation:
The image above shows one possible placement of rectangles to cover the points:
- A rectangle with a lower end at
(0, 0)and its upper end at(2, 2) - A rectangle with a lower end at
(3, 0)and its upper end at(5, 5) - A rectangle with a lower end at
(6, 0)and its upper end at(6, 6)
Example 3:

Input: points = [[2,3],[1,2]], w = 0
Output: 2
Explanation:
The image above shows one possible placement of rectangles to cover the points:
- A rectangle with a lower end at
(1, 0)and its upper end at(1, 2) - A rectangle with a lower end at
(2, 0)and its upper end at(2, 3)
Constraints:
1 <= points.length <= 105points[i].length == 20 <= xi == points[i][0] <= 1090 <= yi == points[i][1] <= 1090 <= w <= 109- All pairs
(xi, yi)are distinct.
Solutions
Solution 1: Greedy + Sorting
According to the problem description, we don’t need to consider the height of the rectangle, only the width.
We can sort all the points according to the x-coordinate and use a variable $x_1$ to record the current x-coordinate of the lower left corner of the rectangle. Then we traverse all the points. If the x-coordinate $x$ of the current point is greater than $x_1 + w$, it means that the current point cannot be covered by the current rectangle. We need to add a new rectangle and update $x_1$ to the x-coordinate of the current point.
After the traversal, we get the minimum number of rectangles needed.
The time complexity is $O(n \times \log n)$, and the space complexity is $O(\log n)$, where $n$ is the number of points.
-
class Solution { public int minRectanglesToCoverPoints(int[][] points, int w) { Arrays.sort(points, (a, b) -> a[0] - b[0]); int ans = 0; int x1 = -(1 << 30); for (int[] p : points) { int x = p[0]; if (x1 + w < x) { x1 = x; ++ans; } } return ans; } } -
class Solution { public: int minRectanglesToCoverPoints(vector<vector<int>>& points, int w) { sort(points.begin(), points.end()); int ans = 0, x1 = -(1 << 30); for (auto& p : points) { int x = p[0]; if (x1 + w < x) { x1 = x; ++ans; } } return ans; } }; -
class Solution: def minRectanglesToCoverPoints(self, points: List[List[int]], w: int) -> int: points.sort() ans, x1 = 0, -inf for x, _ in points: if x1 + w < x: x1 = x ans += 1 return ans -
func minRectanglesToCoverPoints(points [][]int, w int) (ans int) { sort.Slice(points, func(i, j int) bool { return points[i][0] < points[j][0] }) x1 := -(1 << 30) for _, p := range points { if x := p[0]; x1+w < x { x1 = x ans++ } } return } -
function minRectanglesToCoverPoints(points: number[][], w: number): number { points.sort((a, b) => a[0] - b[0]); let ans = 0; let x1 = -Infinity; for (const [x, _] of points) { if (x1 + w < x) { x1 = x; ++ans; } } return ans; }