Welcome to Subscribe On Youtube

3100. Water Bottles II

Description

You are given two integers numBottles and numExchange.

numBottles represents the number of full water bottles that you initially have. In one operation, you can perform one of the following operations:

  • Drink any number of full water bottles turning them into empty bottles.
  • Exchange numExchange empty bottles with one full water bottle. Then, increase numExchange by one.

Note that you cannot exchange multiple batches of empty bottles for the same value of numExchange. For example, if numBottles == 3 and numExchange == 1, you cannot exchange 3 empty water bottles for 3 full bottles.

Return the maximum number of water bottles you can drink.

 

Example 1:

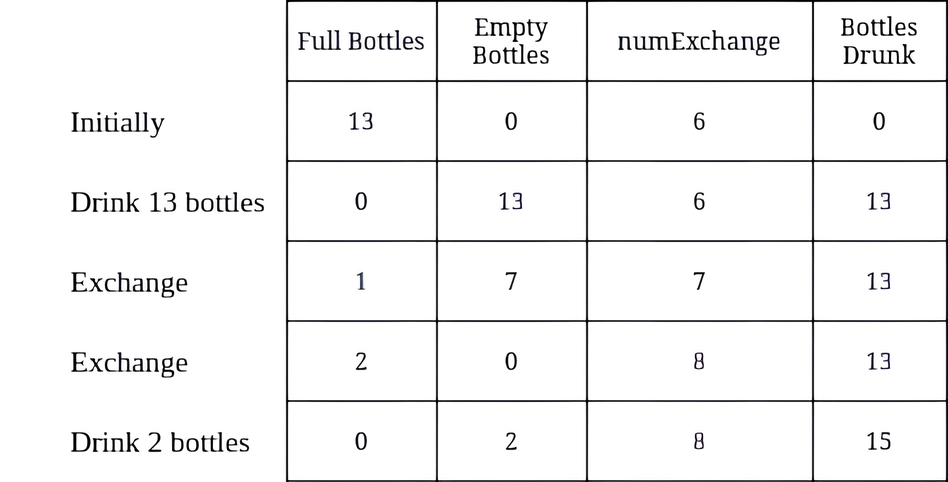
Input: numBottles = 13, numExchange = 6
Output: 15
Explanation: The table above shows the number of full water bottles, empty water bottles, the value of numExchange, and the number of bottles drunk.

Example 2:

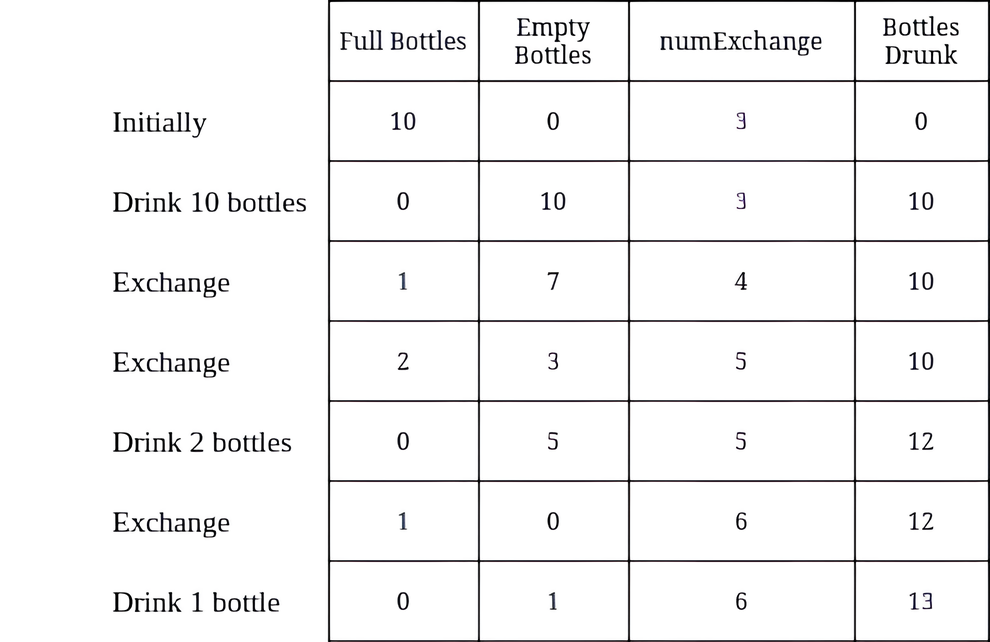
Input: numBottles = 10, numExchange = 3
Output: 13
Explanation: The table above shows the number of full water bottles, empty water bottles, the value of numExchange, and the number of bottles drunk.

 

Constraints:

  • 1 <= numBottles <= 100
  • 1 <= numExchange <= 100

Solutions

Solution 1: Simulation

We can drink all the full water bottles at the beginning, so the initial amount of water we drink is numBottles. Then we continuously perform the following operations:

  • If we currently have numExchange empty water bottles, we can exchange them for a full water bottle, after which the value of numExchange increases by 1. Then, we drink this bottle of water, the amount of water we drink increases by $1$, and the number of empty water bottles increases by $1$.
  • If we currently do not have numExchange empty water bottles, then we can no longer exchange for water, at which point we can stop the operation.

We continuously perform the above operations until we can no longer exchange for water. The final amount of water we drink is the answer.

The time complexity is $O(\sqrt{numBottles})$ and the space complexity is $O(1)$.

  • class Solution {
    public int maxBottlesDrunk(int numBottles, int numExchange) {
        int ans = numBottles;
        while (numBottles >= numExchange) {
            numBottles -= numExchange;
            ++numExchange;
            ++ans;
            ++numBottles;
        }
        return ans;
    }
}

  • class Solution {
public:
    int maxBottlesDrunk(int numBottles, int numExchange) {
        int ans = numBottles;
        while (numBottles >= numExchange) {
            numBottles -= numExchange;
            ++numExchange;
            ++ans;
            ++numBottles;
        }
        return ans;
    }
};

  • class Solution:
    def maxBottlesDrunk(self, numBottles: int, numExchange: int) -> int:
        ans = numBottles
        while numBottles >= numExchange:
            numBottles -= numExchange
            numExchange += 1
            ans += 1
            numBottles += 1
        return ans


  • func maxBottlesDrunk(numBottles int, numExchange int) int {
	ans := numBottles
	for numBottles >= numExchange {
		numBottles -= numExchange
		numExchange++
		ans++
		numBottles++
	}
	return ans
}

  • function maxBottlesDrunk(numBottles: number, numExchange: number): number {
    let ans = numBottles;
    while (numBottles >= numExchange) {
        numBottles -= numExchange;
        ++numExchange;
        ++ans;
        ++numBottles;
    }
    return ans;
}


  • impl Solution {
    pub fn max_bottles_drunk(mut num_bottles: i32, mut num_exchange: i32) -> i32 {
        let mut ans = num_bottles;

        while num_bottles >= num_exchange {
            num_bottles -= num_exchange;
            num_exchange += 1;
            ans += 1;
            num_bottles += 1;
        }

        ans
    }
}

All Problems

All Solutions