Welcome to Subscribe On Youtube
3070. Count Submatrices with Top-Left Element and Sum Less Than k
Description
You are given a 0-indexed integer matrix grid and an integer k.
Return the number of submatrices that contain the top-left element of the grid, and have a sum less than or equal to k.
Example 1:
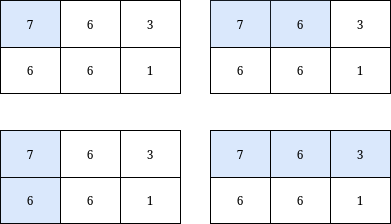
Input: grid = [[7,6,3],[6,6,1]], k = 18 Output: 4 Explanation: There are only 4 submatrices, shown in the image above, that contain the top-left element of grid, and have a sum less than or equal to 18.
Example 2:
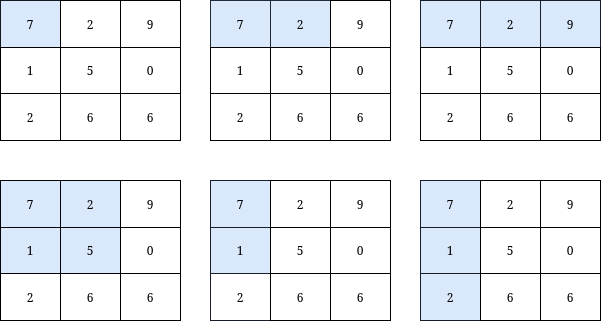
Input: grid = [[7,2,9],[1,5,0],[2,6,6]], k = 20 Output: 6 Explanation: There are only 6 submatrices, shown in the image above, that contain the top-left element of grid, and have a sum less than or equal to 20.
Constraints:
m == grid.lengthn == grid[i].length1 <= n, m <= 10000 <= grid[i][j] <= 10001 <= k <= 109
Solutions
Solution 1: Two-Dimensional Prefix Sum
The problem is actually asking for the number of prefix submatrices in a two-dimensional matrix whose sum is less than or equal to $k$.
The calculation formula for the two-dimensional prefix sum is:
\[s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + x\]The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$, where $m$ and $n$ are the number of rows and columns of the matrix, respectively.
-
class Solution { public int countSubmatrices(int[][] grid, int k) { int m = grid.length, n = grid[0].length; int[][] s = new int[m + 1][n + 1]; int ans = 0; for (int i = 1; i <= m; ++i) { for (int j = 1; j <= n; ++j) { s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + grid[i - 1][j - 1]; if (s[i][j] <= k) { ++ans; } } } return ans; } } -
class Solution { public: int countSubmatrices(vector<vector<int>>& grid, int k) { int m = grid.size(), n = grid[0].size(); int s[m + 1][n + 1]; memset(s, 0, sizeof(s)); int ans = 0; for (int i = 1; i <= m; ++i) { for (int j = 1; j <= n; ++j) { s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + grid[i - 1][j - 1]; if (s[i][j] <= k) { ++ans; } } } return ans; } }; -
class Solution: def countSubmatrices(self, grid: List[List[int]], k: int) -> int: s = [[0] * (len(grid[0]) + 1) for _ in range(len(grid) + 1)] ans = 0 for i, row in enumerate(grid, 1): for j, x in enumerate(row, 1): s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + x ans += s[i][j] <= k return ans -
func countSubmatrices(grid [][]int, k int) (ans int) { s := make([][]int, len(grid)+1) for i := range s { s[i] = make([]int, len(grid[0])+1) } for i, row := range grid { for j, x := range row { s[i+1][j+1] = s[i+1][j] + s[i][j+1] - s[i][j] + x if s[i+1][j+1] <= k { ans++ } } } return } -
function countSubmatrices(grid: number[][], k: number): number { const m = grid.length; const n = grid[0].length; const s: number[][] = Array.from({ length: m + 1 }, () => Array(n + 1).fill(0)); let ans: number = 0; for (let i = 1; i <= m; ++i) { for (let j = 1; j <= n; ++j) { s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + grid[i - 1][j - 1]; if (s[i][j] <= k) { ++ans; } } } return ans; }