Welcome to Subscribe On Youtube

3047. Find the Largest Area of Square Inside Two Rectangles

Description

There exist n rectangles in a 2D plane. You are given two 0-indexed 2D integer arrays bottomLeft and topRight, both of size n x 2, where bottomLeft[i] and topRight[i] represent the bottom-left and top-right coordinates of the ith rectangle respectively.

You can select a region formed from the intersection of two of the given rectangles. You need to find the largest area of a square that can fit inside this region if you select the region optimally.

Return the largest possible area of a square, or 0 if there do not exist any intersecting regions between the rectangles.

 

Example 1:

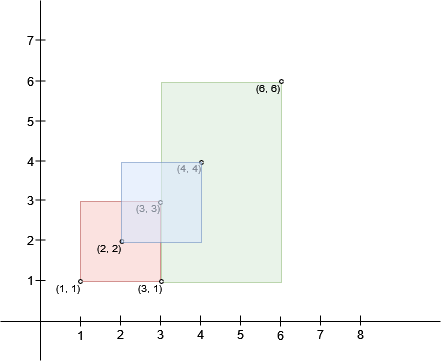
Input: bottomLeft = [[1,1],[2,2],[3,1]], topRight = [[3,3],[4,4],[6,6]]
Output: 1
Explanation: A square with side length 1 can fit inside either the intersecting region of rectangle 0 and rectangle 1, or the intersecting region of rectangle 1 and rectangle 2. Hence the largest area is side * side which is 1 * 1 == 1.
It can be shown that a square with a greater side length can not fit inside any intersecting region.

Example 2:

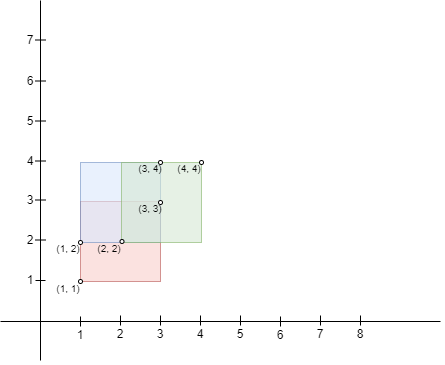
Input: bottomLeft = [[1,1],[2,2],[1,2]], topRight = [[3,3],[4,4],[3,4]]
Output: 1
Explanation: A square with side length 1 can fit inside either the intersecting region of rectangle 0 and rectangle 1, the intersecting region of rectangle 1 and rectangle 2, or the intersection region of all 3 rectangles. Hence the largest area is side * side which is 1 * 1 == 1.
It can be shown that a square with a greater side length can not fit inside any intersecting region.
Note that the region can be formed by the intersection of more than 2 rectangles.

Example 3:

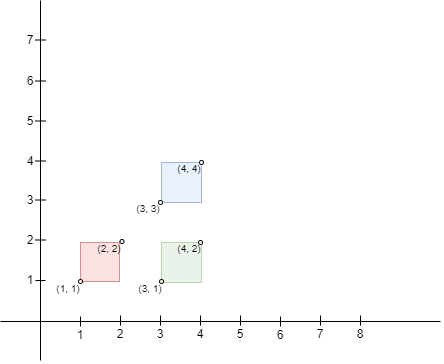
Input: bottomLeft = [[1,1],[3,3],[3,1]], topRight = [[2,2],[4,4],[4,2]]
Output: 0
Explanation: No pair of rectangles intersect, hence, we return 0.

 

Constraints:

  • n == bottomLeft.length == topRight.length
  • 2 <= n <= 103
  • bottomLeft[i].length == topRight[i].length == 2
  • 1 <= bottomLeft[i][0], bottomLeft[i][1] <= 107
  • 1 <= topRight[i][0], topRight[i][1] <= 107
  • bottomLeft[i][0] < topRight[i][0]
  • bottomLeft[i][1] < topRight[i][1]

Solutions

Solution 1

  • class Solution {
    public long largestSquareArea(int[][] bottomLeft, int[][] topRight) {
        long ans = 0;
        for (int i = 0; i < bottomLeft.length; ++i) {
            int x1 = bottomLeft[i][0], y1 = bottomLeft[i][1];
            int x2 = topRight[i][0], y2 = topRight[i][1];
            for (int j = i + 1; j < bottomLeft.length; ++j) {
                int x3 = bottomLeft[j][0], y3 = bottomLeft[j][1];
                int x4 = topRight[j][0], y4 = topRight[j][1];
                int w = Math.min(x2, x4) - Math.max(x1, x3);
                int h = Math.min(y2, y4) - Math.max(y1, y3);
                int e = Math.min(w, h);
                if (e > 0) {
                    ans = Math.max(ans, 1L * e * e);
                }
            }
        }
        return ans;
    }
}

  • class Solution {
public:
    long long largestSquareArea(vector<vector<int>>& bottomLeft, vector<vector<int>>& topRight) {
        long long ans = 0;
        for (int i = 0; i < bottomLeft.size(); ++i) {
            int x1 = bottomLeft[i][0], y1 = bottomLeft[i][1];
            int x2 = topRight[i][0], y2 = topRight[i][1];
            for (int j = i + 1; j < bottomLeft.size(); ++j) {
                int x3 = bottomLeft[j][0], y3 = bottomLeft[j][1];
                int x4 = topRight[j][0], y4 = topRight[j][1];
                int w = min(x2, x4) - max(x1, x3);
                int h = min(y2, y4) - max(y1, y3);
                int e = min(w, h);
                if (e > 0) {
                    ans = max(ans, 1LL * e * e);
                }
            }
        }
        return ans;
    }
};

  • class Solution:
    def largestSquareArea(
        self, bottomLeft: List[List[int]], topRight: List[List[int]]
    ) -> int:
        ans = 0
        for ((x1, y1), (x2, y2)), ((x3, y3), (x4, y4)) in combinations(
            zip(bottomLeft, topRight), 2
        ):
            w = min(x2, x4) - max(x1, x3)
            h = min(y2, y4) - max(y1, y3)
            e = min(w, h)
            if e > 0:
                ans = max(ans, e * e)
        return ans


  • func largestSquareArea(bottomLeft [][]int, topRight [][]int) (ans int64) {
	for i, b1 := range bottomLeft {
		t1 := topRight[i]
		x1, y1 := b1[0], b1[1]
		x2, y2 := t1[0], t1[1]
		for j := i + 1; j < len(bottomLeft); j++ {
			x3, y3 := bottomLeft[j][0], bottomLeft[j][1]
			x4, y4 := topRight[j][0], topRight[j][1]
			w := min(x2, x4) - max(x1, x3)
			h := min(y2, y4) - max(y1, y3)
			e := min(w, h)
			if e > 0 {
				ans = max(ans, int64(e)*int64(e))
			}
		}
	}
	return
}

  • function largestSquareArea(bottomLeft: number[][], topRight: number[][]): number {
    let ans = 0;
    for (let i = 0; i < bottomLeft.length; ++i) {
        const [x1, y1] = bottomLeft[i];
        const [x2, y2] = topRight[i];
        for (let j = i + 1; j < bottomLeft.length; ++j) {
            const [x3, y3] = bottomLeft[j];
            const [x4, y4] = topRight[j];
            const w = Math.min(x2, x4) - Math.max(x1, x3);
            const h = Math.min(y2, y4) - Math.max(y1, y3);
            const e = Math.min(w, h);
            if (e > 0) {
                ans = Math.max(ans, e * e);
            }
        }
    }
    return ans;
}

All Problems

All Solutions