Welcome to Subscribe On Youtube
3027. Find the Number of Ways to Place People II
Description
You are given a 2D array points of size n x 2 representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].
We define the right direction as positive x-axis (increasing x-coordinate) and the left direction as negative x-axis (decreasing x-coordinate). Similarly, we define the up direction as positive y-axis (increasing y-coordinate) and the down direction as negative y-axis (decreasing y-coordinate)
You have to place n people, including Chisato and Takina, at these points such that there is exactly one person at every point. Chisato wants to be alone with Takina, so Chisato will build a rectangular fence with Chisato's position as the upper left corner and Takina's position as the lower right corner of the fence (Note that the fence might not enclose any area, i.e. it can be a line). If any person other than Chisato and Takina is either inside the fence or on the fence, Chisato will be sad.
Return the number of pairs of points where you can place Chisato and Takina, such that Chisato does not become sad on building the fence.
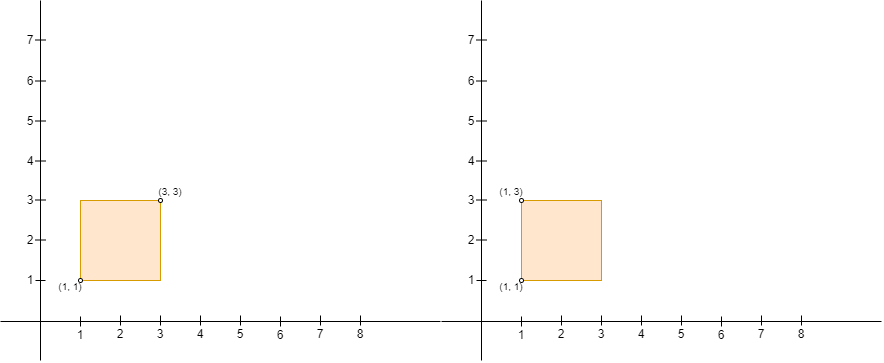
Note that Chisato can only build a fence with Chisato's position as the upper left corner, and Takina's position as the lower right corner. For example, Chisato cannot build either of the fences in the picture below with four corners (1, 1), (1, 3), (3, 1), and (3, 3), because:
- With Chisato at
(3, 3)and Takina at(1, 1), Chisato's position is not the upper left corner and Takina's position is not the lower right corner of the fence. - With Chisato at
(1, 3)and Takina at(1, 1), Takina's position is not the lower right corner of the fence.
Example 1:
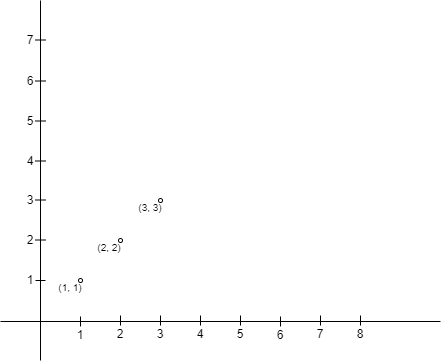
Input: points = [[1,1],[2,2],[3,3]] Output: 0 Explanation: There is no way to place Chisato and Takina such that Chisato can build a fence with Chisato's position as the upper left corner and Takina's position as the lower right corner. Hence we return 0.
Example 2:
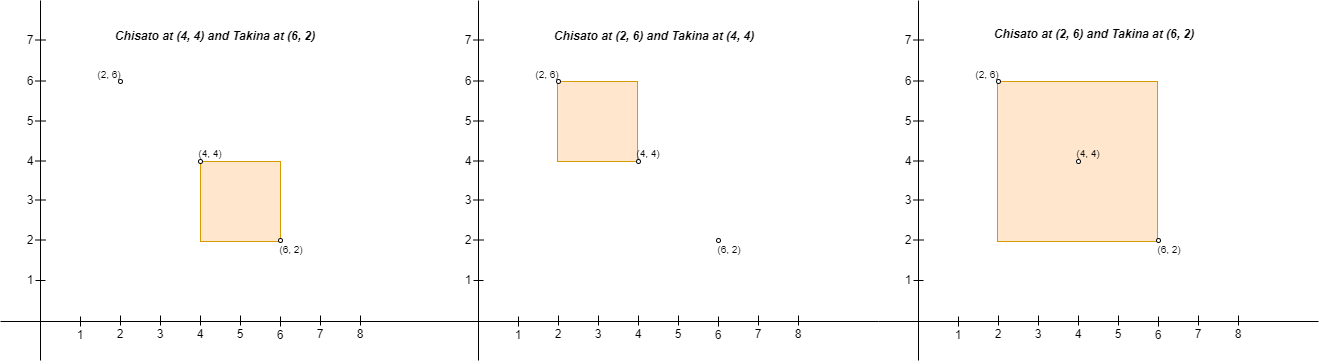
Input: points = [[6,2],[4,4],[2,6]] Output: 2 Explanation: There are two ways to place Chisato and Takina such that Chisato will not be sad: - Place Chisato at (4, 4) and Takina at (6, 2). - Place Chisato at (2, 6) and Takina at (4, 4). You cannot place Chisato at (2, 6) and Takina at (6, 2) because the person at (4, 4) will be inside the fence.
Example 3:
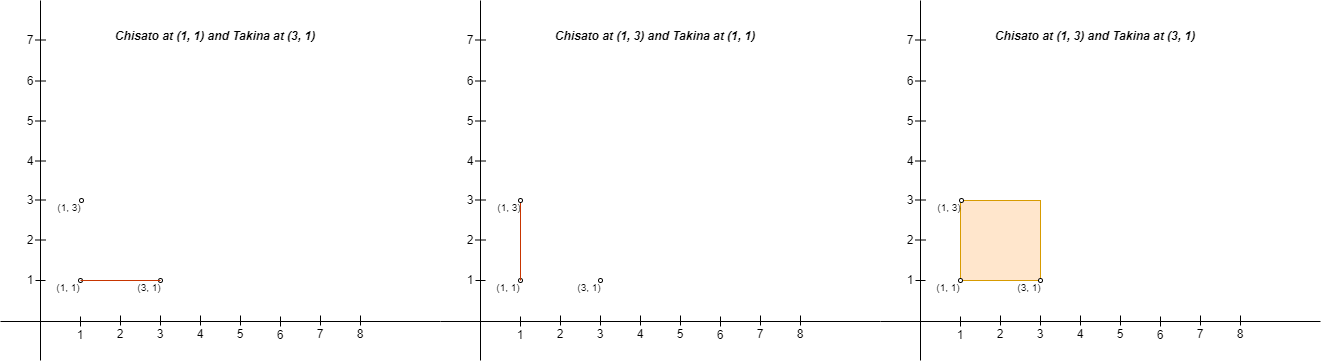
Input: points = [[3,1],[1,3],[1,1]] Output: 2 Explanation: There are two ways to place Chisato and Takina such that Chisato will not be sad: - Place Chisato at (1, 1) and Takina at (3, 1). - Place Chisato at (1, 3) and Takina at (1, 1). You cannot place Chisato at (1, 3) and Takina at (3, 1) because the person at (1, 1) will be on the fence. Note that it does not matter if the fence encloses any area, the first and second fences in the image are valid.
Constraints:
2 <= n <= 1000points[i].length == 2-109 <= points[i][0], points[i][1] <= 109- All
points[i]are distinct.
Solutions
Solution 1: Sorting and Classification
First, we sort the array. Then, we can classify the results based on the properties of a triangle.
- If the sum of the two smaller numbers is less than or equal to the largest number, it cannot form a triangle. Return “Invalid”.
- If the three numbers are equal, it is an equilateral triangle. Return “Equilateral”.
- If two numbers are equal, it is an isosceles triangle. Return “Isosceles”.
- If none of the above conditions are met, it is a scalene triangle. Return “Scalene”.
The time complexity is $O(1)$, and the space complexity is $O(1)$.
-
class Solution { public int numberOfPairs(int[][] points) { Arrays.sort(points, (a, b) -> a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]); int ans = 0; int n = points.length; final int inf = 1 << 30; for (int i = 0; i < n; ++i) { int y1 = points[i][1]; int maxY = -inf; for (int j = i + 1; j < n; ++j) { int y2 = points[j][1]; if (maxY < y2 && y2 <= y1) { maxY = y2; ++ans; } } } return ans; } } -
class Solution { public: int numberOfPairs(vector<vector<int>>& points) { sort(points.begin(), points.end(), [](const vector<int>& a, const vector<int>& b) { return a[0] < b[0] || (a[0] == b[0] && b[1] < a[1]); }); int n = points.size(); int ans = 0; for (int i = 0; i < n; ++i) { int y1 = points[i][1]; int maxY = INT_MIN; for (int j = i + 1; j < n; ++j) { int y2 = points[j][1]; if (maxY < y2 && y2 <= y1) { maxY = y2; ++ans; } } } return ans; } }; -
class Solution: def numberOfPairs(self, points: List[List[int]]) -> int: points.sort(key=lambda x: (x[0], -x[1])) ans = 0 for i, (_, y1) in enumerate(points): max_y = -inf for _, y2 in points[i + 1 :]: if max_y < y2 <= y1: max_y = y2 ans += 1 return ans -
func numberOfPairs(points [][]int) (ans int) { sort.Slice(points, func(i, j int) bool { return points[i][0] < points[j][0] || points[i][0] == points[j][0] && points[j][1] < points[i][1] }) for i, p1 := range points { y1 := p1[1] maxY := math.MinInt32 for _, p2 := range points[i+1:] { y2 := p2[1] if maxY < y2 && y2 <= y1 { maxY = y2 ans++ } } } return } -
function numberOfPairs(points: number[][]): number { points.sort((a, b) => (a[0] === b[0] ? b[1] - a[1] : a[0] - b[0])); const n = points.length; let ans = 0; for (let i = 0; i < n; ++i) { const [_, y1] = points[i]; let maxY = -Infinity; for (let j = i + 1; j < n; ++j) { const [_, y2] = points[j]; if (maxY < y2 && y2 <= y1) { maxY = y2; ++ans; } } } return ans; } -
public class Solution { public int NumberOfPairs(int[][] points) { Array.Sort(points, (a, b) => a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]); int ans = 0; int n = points.Length; int inf = 1 << 30; for (int i = 0; i < n; ++i) { int y1 = points[i][1]; int maxY = -inf; for (int j = i + 1; j < n; ++j) { int y2 = points[j][1]; if (maxY < y2 && y2 <= y1) { maxY = y2; ++ans; } } } return ans; } }