Welcome to Subscribe On Youtube
3015. Count the Number of Houses at a Certain Distance I
Description
You are given three positive integers n, x, and y.
In a city, there exist houses numbered 1 to n connected by n streets. There is a street connecting the house numbered i with the house numbered i + 1 for all 1 <= i <= n - 1 . An additional street connects the house numbered x with the house numbered y.
For each k, such that 1 <= k <= n, you need to find the number of pairs of houses (house1, house2) such that the minimum number of streets that need to be traveled to reach house2 from house1 is k.
Return a 1-indexed array result of length n where result[k] represents the total number of pairs of houses such that the minimum streets required to reach one house from the other is k.
Note that x and y can be equal.
Example 1:

Input: n = 3, x = 1, y = 3 Output: [6,0,0] Explanation: Let's look at each pair of houses: - For the pair (1, 2), we can go from house 1 to house 2 directly. - For the pair (2, 1), we can go from house 2 to house 1 directly. - For the pair (1, 3), we can go from house 1 to house 3 directly. - For the pair (3, 1), we can go from house 3 to house 1 directly. - For the pair (2, 3), we can go from house 2 to house 3 directly. - For the pair (3, 2), we can go from house 3 to house 2 directly.
Example 2:
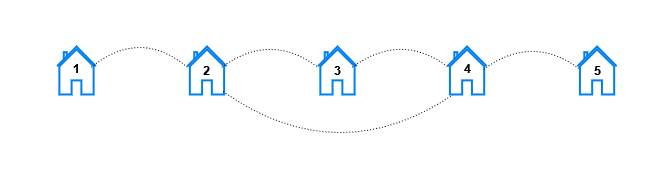
Input: n = 5, x = 2, y = 4 Output: [10,8,2,0,0] Explanation: For each distance k the pairs are: - For k == 1, the pairs are (1, 2), (2, 1), (2, 3), (3, 2), (2, 4), (4, 2), (3, 4), (4, 3), (4, 5), and (5, 4). - For k == 2, the pairs are (1, 3), (3, 1), (1, 4), (4, 1), (2, 5), (5, 2), (3, 5), and (5, 3). - For k == 3, the pairs are (1, 5), and (5, 1). - For k == 4 and k == 5, there are no pairs.
Example 3:
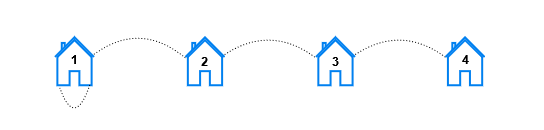
Input: n = 4, x = 1, y = 1 Output: [6,4,2,0] Explanation: For each distance k the pairs are: - For k == 1, the pairs are (1, 2), (2, 1), (2, 3), (3, 2), (3, 4), and (4, 3). - For k == 2, the pairs are (1, 3), (3, 1), (2, 4), and (4, 2). - For k == 3, the pairs are (1, 4), and (4, 1). - For k == 4, there are no pairs.
Constraints:
2 <= n <= 1001 <= x, y <= n
Solutions
Solution 1: Enumeration
| We can enumerate each pair of points $(i, j)$. The shortest distance from $i$ to $j$ is $min( | i - j | , | i - x | + 1 + | j - y | , | i - y | + 1 + | j - x | )$. We add $2$ to the count of this distance because both $(i, j)$ and $(j, i)$ are valid pairs of points. |
The time complexity is $O(n^2)$, where $n$ is the $n$ given in the problem. Ignoring the space consumption of the answer array, the space complexity is $O(1)$.
-
class Solution { public int[] countOfPairs(int n, int x, int y) { int[] ans = new int[n]; x--; y--; for (int i = 0; i < n; ++i) { for (int j = i + 1; j < n; ++j) { int a = j - i; int b = Math.abs(i - x) + 1 + Math.abs(j - y); int c = Math.abs(i - y) + 1 + Math.abs(j - x); ans[Math.min(a, Math.min(b, c)) - 1] += 2; } } return ans; } } -
class Solution { public: vector<int> countOfPairs(int n, int x, int y) { vector<int> ans(n); x--; y--; for (int i = 0; i < n; ++i) { for (int j = i + 1; j < n; ++j) { int a = j - i; int b = abs(x - i) + abs(y - j) + 1; int c = abs(y - i) + abs(x - j) + 1; ans[min({a, b, c}) - 1] += 2; } } return ans; } }; -
class Solution: def countOfPairs(self, n: int, x: int, y: int) -> List[int]: x, y = x - 1, y - 1 ans = [0] * n for i in range(n): for j in range(i + 1, n): a = j - i b = abs(i - x) + 1 + abs(j - y) c = abs(i - y) + 1 + abs(j - x) ans[min(a, b, c) - 1] += 2 return ans -
func countOfPairs(n int, x int, y int) []int { ans := make([]int, n) x, y = x-1, y-1 for i := 0; i < n; i++ { for j := i + 1; j < n; j++ { a := j - i b := abs(x-i) + abs(y-j) + 1 c := abs(x-j) + abs(y-i) + 1 ans[min(a, min(b, c))-1] += 2 } } return ans } func abs(x int) int { if x < 0 { return -x } return x } -
function countOfPairs(n: number, x: number, y: number): number[] { const ans: number[] = Array(n).fill(0); x--; y--; for (let i = 0; i < n; ++i) { for (let j = i + 1; j < n; ++j) { const a = j - i; const b = Math.abs(x - i) + Math.abs(y - j) + 1; const c = Math.abs(y - i) + Math.abs(x - j) + 1; ans[Math.min(a, b, c) - 1] += 2; } } return ans; }