Welcome to Subscribe On Youtube
3004. Maximum Subtree of the Same Color
Description
You are given a 2D integer array edges representing a tree with n nodes, numbered from 0 to n - 1, rooted at node 0, where edges[i] = [ui, vi] means there is an edge between the nodes vi and ui.
You are also given a 0-indexed integer array colors of size n, where colors[i] is the color assigned to node i.
We want to find a node v such that every node in the subtree of v has the same color.
Return the size of such subtree with the maximum number of nodes possible.
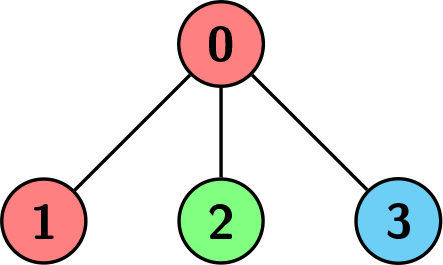
Example 1:
Input: edges = [[0,1],[0,2],[0,3]], colors = [1,1,2,3] Output: 1 Explanation: Each color is represented as: 1 -> Red, 2 -> Green, 3 -> Blue. We can see that the subtree rooted at node 0 has children with different colors. Any other subtree is of the same color and has a size of 1. Hence, we return 1.
Example 2:
Input: edges = [[0,1],[0,2],[0,3]], colors = [1,1,1,1] Output: 4 Explanation: The whole tree has the same color, and the subtree rooted at node 0 has the most number of nodes which is 4. Hence, we return 4.
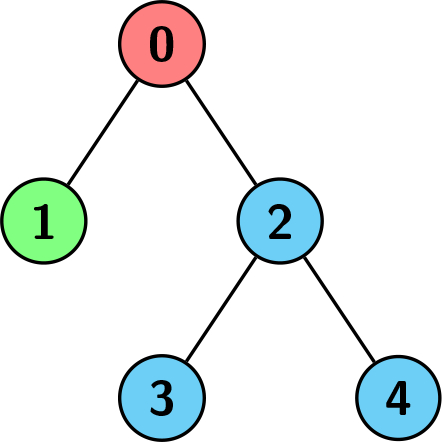
Example 3:
Input: edges = [[0,1],[0,2],[2,3],[2,4]], colors = [1,2,3,3,3] Output: 3 Explanation: Each color is represented as: 1 -> Red, 2 -> Green, 3 -> Blue. We can see that the subtree rooted at node 0 has children with different colors. Any other subtree is of the same color, but the subtree rooted at node 2 has a size of 3 which is the maximum. Hence, we return 3.
Constraints:
n == edges.length + 11 <= n <= 5 * 104edges[i] == [ui, vi]0 <= ui, vi < ncolors.length == n1 <= colors[i] <= 105- The input is generated such that the graph represented by
edgesis a tree.
Solutions
Solution 1: DFS
First, according to the edge information given in the problem, we construct an adjacency list $g$, where $g[a]$ represents all adjacent nodes of node $a$. Then we create an array $size$ of length $n$, where $size[a]$ represents the number of nodes in the subtree with node $a$ as the root.
Next, we design a function $dfs(a, fa)$, which will return whether the subtree with node $a$ as the root meets the requirements of the problem. The execution process of the function $dfs(a, fa)$ is as follows:
- First, we use a variable $ok$ to record whether the subtree with node $a$ as the root meets the requirements of the problem, and initially $ok$ is $true$.
- Then, we traverse all adjacent nodes $b$ of node $a$. If $b$ is not the parent node $fa$ of $a$, then we recursively call $dfs(b, a)$, save the return value into the variable $t$, and update $ok$ to the value of $ok$ and $colors[a] = colors[b] \land t$, where $\land$ represents logical AND operation. Then, we update $size[a] = size[a] + size[b]$.
- After that, we judge the value of $ok$. If $ok$ is $true$, then we update the answer $ans = \max(ans, size[a])$.
- Finally, we return the value of $ok$.
We call $dfs(0, -1)$, where $0$ represents the root node number, and $-1$ represents that the root node has no parent node. The final answer is $ans$.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Where $n$ is the number of nodes.
-
class Solution { private List<Integer>[] g; private int[] colors; private int[] size; private int ans; public int maximumSubtreeSize(int[][] edges, int[] colors) { int n = edges.length + 1; g = new List[n]; size = new int[n]; this.colors = colors; Arrays.fill(size, 1); Arrays.setAll(g, i -> new ArrayList<>()); for (var e : edges) { int a = e[0], b = e[1]; g[a].add(b); g[b].add(a); } dfs(0, -1); return ans; } private boolean dfs(int a, int fa) { boolean ok = true; for (int b : g[a]) { if (b != fa) { boolean t = dfs(b, a); ok = ok && colors[a] == colors[b] && t; size[a] += size[b]; } } if (ok) { ans = Math.max(ans, size[a]); } return ok; } } -
class Solution { public: int maximumSubtreeSize(vector<vector<int>>& edges, vector<int>& colors) { int n = edges.size() + 1; vector<int> g[n]; vector<int> size(n, 1); for (auto& e : edges) { int a = e[0], b = e[1]; g[a].push_back(b); g[b].push_back(a); } int ans = 0; function<bool(int, int)> dfs = [&](int a, int fa) { bool ok = true; for (int b : g[a]) { if (b != fa) { bool t = dfs(b, a); ok = ok && colors[a] == colors[b] && t; size[a] += size[b]; } } if (ok) { ans = max(ans, size[a]); } return ok; }; dfs(0, -1); return ans; } }; -
class Solution: def maximumSubtreeSize(self, edges: List[List[int]], colors: List[int]) -> int: def dfs(a: int, fa: int) -> bool: ok = True for b in g[a]: if b != fa: t = dfs(b, a) ok = ok and colors[a] == colors[b] and t size[a] += size[b] if ok: nonlocal ans ans = max(ans, size[a]) return ok n = len(edges) + 1 g = [[] for _ in range(n)] size = [1] * n for a, b in edges: g[a].append(b) g[b].append(a) ans = 0 dfs(0, -1) return ans -
func maximumSubtreeSize(edges [][]int, colors []int) (ans int) { n := len(edges) + 1 g := make([][]int, n) for _, e := range edges { a, b := e[0], e[1] g[a] = append(g[a], b) g[b] = append(g[b], a) } size := make([]int, n) var dfs func(int, int) bool dfs = func(a, fa int) bool { size[a] = 1 ok := true for _, b := range g[a] { if b != fa { t := dfs(b, a) ok = ok && t && colors[a] == colors[b] size[a] += size[b] } } if ok { ans = max(ans, size[a]) } return ok } dfs(0, -1) return } -
function maximumSubtreeSize(edges: number[][], colors: number[]): number { const n = edges.length + 1; const g: number[][] = Array.from({ length: n }, () => []); for (const [a, b] of edges) { g[a].push(b); g[b].push(a); } const size: number[] = Array(n).fill(1); let ans = 0; const dfs = (a: number, fa: number): boolean => { let ok = true; for (const b of g[a]) { if (b !== fa) { const t = dfs(b, a); ok = ok && t && colors[a] === colors[b]; size[a] += size[b]; } } if (ok) { ans = Math.max(ans, size[a]); } return ok; }; dfs(0, -1); return ans; }