Welcome to Subscribe On Youtube
2924. Find Champion II
Description
There are n teams numbered from 0 to n - 1 in a tournament; each team is also a node in a DAG.
You are given the integer n and a 0-indexed 2D integer array edges of length m representing the DAG, where edges[i] = [ui, vi] indicates that there is a directed edge from team ui to team vi in the graph.
A directed edge from a to b in the graph means that team a is stronger than team b and team b is weaker than team a.
Team a will be the champion of the tournament if there is no team b that is stronger than team a.
Return the team that will be the champion of the tournament if there is a unique champion, otherwise, return -1.
Notes
- A cycle is a series of nodes
a1, a2, ..., an, an+1such that nodea1is the same node as nodean+1, the nodesa1, a2, ..., anare distinct, and there is a directed edge from the nodeaito nodeai+1for everyiin the range[1, n]. - A DAG is a directed graph that does not have any cycle.
Example 1:
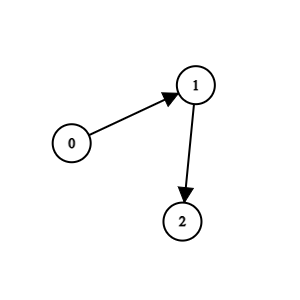
Input: n = 3, edges = [[0,1],[1,2]] Output: 0 Explanation: Team 1 is weaker than team 0. Team 2 is weaker than team 1. So the champion is team 0.
Example 2:
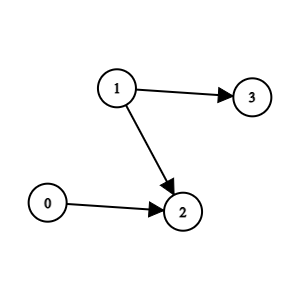
Input: n = 4, edges = [[0,2],[1,3],[1,2]] Output: -1 Explanation: Team 2 is weaker than team 0 and team 1. Team 3 is weaker than team 1. But team 1 and team 0 are not weaker than any other teams. So the answer is -1.
Constraints:
1 <= n <= 100m == edges.length0 <= m <= n * (n - 1) / 2edges[i].length == 20 <= edge[i][j] <= n - 1edges[i][0] != edges[i][1]- The input is generated such that if team
ais stronger than teamb, teambis not stronger than teama. - The input is generated such that if team
ais stronger than teamband teambis stronger than teamc, then teamais stronger than teamc.
Solutions
Solution 1: Counting In-degrees
Based on the problem description, we only need to count the in-degrees of each node and record them in an array $indeg$. If only one node has an in-degree of $0$, then this node is the champion; otherwise, there is no unique champion.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes.
-
class Solution { public int findChampion(int n, int[][] edges) { int[] indeg = new int[n]; for (var e : edges) { ++indeg[e[1]]; } int ans = -1, cnt = 0; for (int i = 0; i < n; ++i) { if (indeg[i] == 0) { ++cnt; ans = i; } } return cnt == 1 ? ans : -1; } } -
class Solution { public: int findChampion(int n, vector<vector<int>>& edges) { int indeg[n]; memset(indeg, 0, sizeof(indeg)); for (auto& e : edges) { ++indeg[e[1]]; } int ans = -1, cnt = 0; for (int i = 0; i < n; ++i) { if (indeg[i] == 0) { ++cnt; ans = i; } } return cnt == 1 ? ans : -1; } }; -
class Solution: def findChampion(self, n: int, edges: List[List[int]]) -> int: indeg = [0] * n for _, v in edges: indeg[v] += 1 return -1 if indeg.count(0) != 1 else indeg.index(0) -
func findChampion(n int, edges [][]int) int { indeg := make([]int, n) for _, e := range edges { indeg[e[1]]++ } ans, cnt := -1, 0 for i, x := range indeg { if x == 0 { cnt++ ans = i } } if cnt == 1 { return ans } return -1 } -
function findChampion(n: number, edges: number[][]): number { const indeg: number[] = Array(n).fill(0); for (const [_, v] of edges) { ++indeg[v]; } let [ans, cnt] = [-1, 0]; for (let i = 0; i < n; ++i) { if (indeg[i] === 0) { ++cnt; ans = i; } } return cnt === 1 ? ans : -1; }