2867. Count Valid Paths in a Tree

Description

There is an undirected tree with n nodes labeled from 1 to n. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [u_i, v_i] indicates that there is an edge between nodes u_i and v_i in the tree.

Return the number of valid paths in the tree.

A path (a, b) is valid if there exists exactly one prime number among the node labels in the path from a to b.

Note that:

The path (a, b) is a sequence of distinct nodes starting with node a and ending with node b such that every two adjacent nodes in the sequence share an edge in the tree.
Path (a, b) and path (b, a) are considered the same and counted only once.

Example 1:

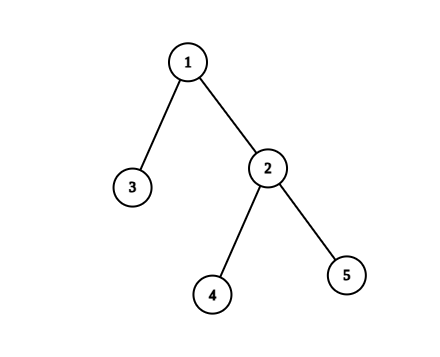
Input: n = 5, edges = [[1,2],[1,3],[2,4],[2,5]]
Output: 4
Explanation: The pairs with exactly one prime number on the path between them are: 
- (1, 2) since the path from 1 to 2 contains prime number 2. 
- (1, 3) since the path from 1 to 3 contains prime number 3.
- (1, 4) since the path from 1 to 4 contains prime number 2.
- (2, 4) since the path from 2 to 4 contains prime number 2.
It can be shown that there are only 4 valid paths.

Example 2:

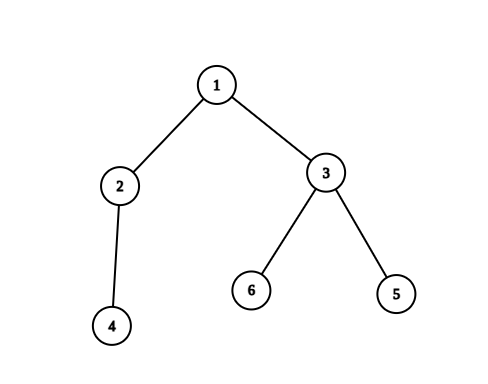
Input: n = 6, edges = [[1,2],[1,3],[2,4],[3,5],[3,6]]
Output: 6
Explanation: The pairs with exactly one prime number on the path between them are: 
- (1, 2) since the path from 1 to 2 contains prime number 2.
- (1, 3) since the path from 1 to 3 contains prime number 3.
- (1, 4) since the path from 1 to 4 contains prime number 2.
- (1, 6) since the path from 1 to 6 contains prime number 3.
- (2, 4) since the path from 2 to 4 contains prime number 2.
- (3, 6) since the path from 3 to 6 contains prime number 3.
It can be shown that there are only 6 valid paths.

Constraints:

1 <= n <= 10⁵
edges.length == n - 1
edges[i].length == 2
1 <= u_i, v_i <= n
The input is generated such that edges represent a valid tree.

Solutions

Solution 1: Preprocessing + Union-Find + Enumeration

We can preprocess to get all the prime numbers in $[1, n]$, where $prime[i]$ indicates whether $i$ is a prime number.

Next, we build a graph $g$ based on the two-dimensional integer array, where $g[i]$ represents all the neighbor nodes of node $i$. If both nodes of an edge are not prime numbers, we merge these two nodes into the same connected component.

Then, we enumerate all prime numbers $i$ in the range of $[1, n]$, considering all paths that include $i$.

Since $i$ is already a prime number, if $i$ is an endpoint of the path, we only need to accumulate the sizes of all connected components adjacent to node $i$. If $i$ is a middle point on the path, we need to accumulate the product of the sizes of any two adjacent connected components.

The time complexity is $O(n \times \alpha(n))$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes, and $\alpha$ is the inverse function of the Ackermann function.

class Solution {
    public long countPaths(int n, int[][] edges) {
        List<Boolean> prime = new ArrayList<>(n + 1);
        for (int i = 0; i <= n; ++i) {
            prime.add(true);
        }
        prime.set(1, false);

        List<Integer> all = new ArrayList<>();
        for (int i = 2; i <= n; ++i) {
            if (prime.get(i)) {
                all.add(i);
            }
            for (int x : all) {
                int temp = i * x;
                if (temp > n) {
                    break;
                }
                prime.set(temp, false);
                if (i % x == 0) {
                    break;
                }
            }
        }

        List<List<Integer>> con = new ArrayList<>(n + 1);
        for (int i = 0; i <= n; ++i) {
            con.add(new ArrayList<>());
        }
        for (int[] e : edges) {
            con.get(e[0]).add(e[1]);
            con.get(e[1]).add(e[0]);
        }

        long[] r = {0};
        dfs(1, 0, con, prime, r);
        return r[0];
    }

    private long mul(long x, long y) {
        return x * y;
    }

    private class Pair {
        int first;
        int second;

        Pair(int first, int second) {
            this.first = first;
            this.second = second;
        }
    }

    private Pair dfs(int x, int f, List<List<Integer>> con, List<Boolean> prime, long[] r) {
        Pair v = new Pair(!prime.get(x) ? 1 : 0, prime.get(x) ? 1 : 0);
        for (int y : con.get(x)) {
            if (y == f) continue;
            Pair p = dfs(y, x, con, prime, r);
            r[0] += mul(p.first, v.second) + mul(p.second, v.first);
            if (prime.get(x)) {
                v.second += p.first;
            } else {
                v.first += p.first;
                v.second += p.second;
            }
        }
        return v;
    }
}

class Solution {
    long long mul(long long x, long long y) {
        return x * y;
    }

    pair<int, int> dfs(int x, int f, const vector<vector<int>>& con, const vector<bool>& prime, long long& r) {
        pair<int, int> v = {!prime[x], prime[x]};
        for (int y : con[x]) {
            if (y == f) continue;
            const auto& p = dfs(y, x, con, prime, r);
            r += mul(p.first, v.second) + mul(p.second, v.first);
            if (prime[x]) {
                v.second += p.first;
            } else {
                v.first += p.first;
                v.second += p.second;
            }
        }
        return v;
    }

public:
    long long countPaths(int n, vector<vector<int>>& edges) {
        vector<bool> prime(n + 1, true);
        prime[1] = false;
        vector<int> all;
        for (int i = 2; i <= n; ++i) {
            if (prime[i]) {
                all.push_back(i);
            }
            for (int x : all) {
                const int temp = i * x;
                if (temp > n) {
                    break;
                }
                prime[temp] = false;
                if (i % x == 0) {
                    break;
                }
            }
        }
        vector<vector<int>> con(n + 1);
        for (const auto& e : edges) {
            con[e[0]].push_back(e[1]);
            con[e[1]].push_back(e[0]);
        }
        long long r = 0;
        dfs(1, 0, con, prime, r);
        return r;
    }
};

class Solution:
    def countPaths(self, n: int, edges: List[List[int]]) -> int:
        def mul(x, y):
            return x * y

        def dfs(x, f, con, prime, r):
            v = [1 - prime[x], prime[x]]
            for y in con[x]:
                if y == f:
                    continue
                p = dfs(y, x, con, prime, r)
                r[0] += mul(p[0], v[1]) + mul(p[1], v[0])
                if prime[x]:
                    v[1] += p[0]
                else:
                    v[0] += p[0]
                    v[1] += p[1]
            return v

        prime = [True] * (n + 1)
        prime[1] = False

        all_primes = []
        for i in range(2, n + 1):
            if prime[i]:
                all_primes.append(i)
            for x in all_primes:
                temp = i * x
                if temp > n:
                    break
                prime[temp] = False
                if i % x == 0:
                    break

        con = [[] for _ in range(n + 1)]
        for e in edges:
            con[e[0]].append(e[1])
            con[e[1]].append(e[0])

        r = [0]
        dfs(1, 0, con, prime, r)
        return r[0]

const mx int = 1e5 + 10

var prime [mx]bool

func init() {
	for i := 2; i < mx; i++ {
		prime[i] = true
	}
	for i := 2; i < mx; i++ {
		if prime[i] {
			for j := i + i; j < mx; j += i {
				prime[j] = false
			}
		}
	}
}

type unionFind struct {
	p, size []int
}

func newUnionFind(n int) *unionFind {
	p := make([]int, n)
	size := make([]int, n)
	for i := range p {
		p[i] = i
		size[i] = 1
	}
	return &unionFind{p, size}
}

func (uf *unionFind) find(x int) int {
	if uf.p[x] != x {
		uf.p[x] = uf.find(uf.p[x])
	}
	return uf.p[x]
}

func (uf *unionFind) union(a, b int) bool {
	pa, pb := uf.find(a), uf.find(b)
	if pa == pb {
		return false
	}
	if uf.size[pa] > uf.size[pb] {
		uf.p[pb] = pa
		uf.size[pa] += uf.size[pb]
	} else {
		uf.p[pa] = pb
		uf.size[pb] += uf.size[pa]
	}
	return true
}

func (uf *unionFind) getSize(x int) int {
	return uf.size[uf.find(x)]
}

func countPaths(n int, edges [][]int) (ans int64) {
	uf := newUnionFind(n + 1)
	g := make([][]int, n+1)
	for _, e := range edges {
		u, v := e[0], e[1]
		g[u] = append(g[u], v)
		g[v] = append(g[v], u)
		if !prime[u] && !prime[v] {
			uf.union(u, v)
		}
	}
	for i := 1; i <= n; i++ {
		if prime[i] {
			t := 0
			for _, j := range g[i] {
				if !prime[j] {
					cnt := uf.getSize(j)
					ans += int64(cnt + cnt*t)
					t += cnt
				}
			}
		}
	}
	return
}

const mx = 100010;
const prime = Array(mx).fill(true);
prime[0] = prime[1] = false;
for (let i = 2; i <= mx; ++i) {
    if (prime[i]) {
        for (let j = i + i; j <= mx; j += i) {
            prime[j] = false;
        }
    }
}

class UnionFind {
    p: number[];
    size: number[];
    constructor(n: number) {
        this.p = Array(n)
            .fill(0)
            .map((_, i) => i);
        this.size = Array(n).fill(1);
    }

    find(x: number): number {
        if (this.p[x] !== x) {
            this.p[x] = this.find(this.p[x]);
        }
        return this.p[x];
    }

    union(a: number, b: number): boolean {
        const [pa, pb] = [this.find(a), this.find(b)];
        if (pa === pb) {
            return false;
        }
        if (this.size[pa] > this.size[pb]) {
            this.p[pb] = pa;
            this.size[pa] += this.size[pb];
        } else {
            this.p[pa] = pb;
            this.size[pb] += this.size[pa];
        }
        return true;
    }

    getSize(x: number): number {
        return this.size[this.find(x)];
    }
}

function countPaths(n: number, edges: number[][]): number {
    const uf = new UnionFind(n + 1);
    const g: number[][] = Array(n + 1)
        .fill(0)
        .map(() => []);
    for (const [u, v] of edges) {
        g[u].push(v);
        g[v].push(u);
        if (!prime[u] && !prime[v]) {
            uf.union(u, v);
        }
    }
    let ans = 0;
    for (let i = 1; i <= n; ++i) {
        if (prime[i]) {
            let t = 0;
            for (let j of g[i]) {
                if (!prime[j]) {
                    const cnt = uf.getSize(j);
                    ans += cnt + t * cnt;
                    t += cnt;
                }
            }
        }
    }
    return ans;
}

2867 - Count Valid Paths in a Tree

2867. Count Valid Paths in a Tree

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

2867. Count Valid Paths in a Tree

Description

Solutions

All Problems

All Solutions