Welcome to Subscribe On Youtube
2858. Minimum Edge Reversals So Every Node Is Reachable
Description
There is a simple directed graph with n nodes labeled from 0 to n - 1. The graph would form a tree if its edges were bi-directional.
You are given an integer n and a 2D integer array edges, where edges[i] = [ui, vi] represents a directed edge going from node ui to node vi.
An edge reversal changes the direction of an edge, i.e., a directed edge going from node ui to node vi becomes a directed edge going from node vi to node ui.
For every node i in the range [0, n - 1], your task is to independently calculate the minimum number of edge reversals required so it is possible to reach any other node starting from node i through a sequence of directed edges.
Return an integer array answer, where answer[i] is the minimum number of edge reversals required so it is possible to reach any other node starting from node i through a sequence of directed edges.
Example 1:
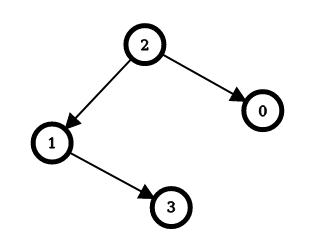
Input: n = 4, edges = [[2,0],[2,1],[1,3]] Output: [1,1,0,2] Explanation: The image above shows the graph formed by the edges. For node 0: after reversing the edge [2,0], it is possible to reach any other node starting from node 0. So, answer[0] = 1. For node 1: after reversing the edge [2,1], it is possible to reach any other node starting from node 1. So, answer[1] = 1. For node 2: it is already possible to reach any other node starting from node 2. So, answer[2] = 0. For node 3: after reversing the edges [1,3] and [2,1], it is possible to reach any other node starting from node 3. So, answer[3] = 2.
Example 2:
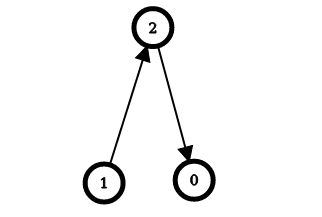
Input: n = 3, edges = [[1,2],[2,0]] Output: [2,0,1] Explanation: The image above shows the graph formed by the edges. For node 0: after reversing the edges [2,0] and [1,2], it is possible to reach any other node starting from node 0. So, answer[0] = 2. For node 1: it is already possible to reach any other node starting from node 1. So, answer[1] = 0. For node 2: after reversing the edge [1, 2], it is possible to reach any other node starting from node 2. So, answer[2] = 1.
Constraints:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ui == edges[i][0] < n0 <= vi == edges[i][1] < nui != vi- The input is generated such that if the edges were bi-directional, the graph would be a tree.
Solutions
-
class Solution { private List<int[]>[] g; private int[] ans; public int[] minEdgeReversals(int n, int[][] edges) { ans = new int[n]; g = new List[n]; Arrays.setAll(g, i -> new ArrayList<>()); for (var e : edges) { int x = e[0], y = e[1]; g[x].add(new int[] {y, 1}); g[y].add(new int[] {x, -1}); } dfs(0, -1); dfs2(0, -1); return ans; } private void dfs(int i, int fa) { for (var ne : g[i]) { int j = ne[0], k = ne[1]; if (j != fa) { ans[0] += k < 0 ? 1 : 0; dfs(j, i); } } } private void dfs2(int i, int fa) { for (var ne : g[i]) { int j = ne[0], k = ne[1]; if (j != fa) { ans[j] = ans[i] + k; dfs2(j, i); } } } } -
class Solution { public: vector<int> minEdgeReversals(int n, vector<vector<int>>& edges) { vector<pair<int, int>> g[n]; vector<int> ans(n); for (auto& e : edges) { int x = e[0], y = e[1]; g[x].emplace_back(y, 1); g[y].emplace_back(x, -1); } function<void(int, int)> dfs = [&](int i, int fa) { for (auto& [j, k] : g[i]) { if (j != fa) { ans[0] += k < 0; dfs(j, i); } } }; function<void(int, int)> dfs2 = [&](int i, int fa) { for (auto& [j, k] : g[i]) { if (j != fa) { ans[j] = ans[i] + k; dfs2(j, i); } } }; dfs(0, -1); dfs2(0, -1); return ans; } }; -
class Solution: def minEdgeReversals(self, n: int, edges: List[List[int]]) -> List[int]: ans = [0] * n g = [[] for _ in range(n)] for x, y in edges: g[x].append((y, 1)) g[y].append((x, -1)) def dfs(i: int, fa: int): for j, k in g[i]: if j != fa: ans[0] += int(k < 0) dfs(j, i) dfs(0, -1) def dfs2(i: int, fa: int): for j, k in g[i]: if j != fa: ans[j] = ans[i] + k dfs2(j, i) dfs2(0, -1) return ans -
func minEdgeReversals(n int, edges [][]int) []int { g := make([][][2]int, n) for _, e := range edges { x, y := e[0], e[1] g[x] = append(g[x], [2]int{y, 1}) g[y] = append(g[y], [2]int{x, -1}) } ans := make([]int, n) var dfs func(int, int) var dfs2 func(int, int) dfs = func(i, fa int) { for _, ne := range g[i] { j, k := ne[0], ne[1] if j != fa { if k < 0 { ans[0]++ } dfs(j, i) } } } dfs2 = func(i, fa int) { for _, ne := range g[i] { j, k := ne[0], ne[1] if j != fa { ans[j] = ans[i] + k dfs2(j, i) } } } dfs(0, -1) dfs2(0, -1) return ans } -
function minEdgeReversals(n: number, edges: number[][]): number[] { const g: number[][][] = Array.from({ length: n }, () => []); for (const [x, y] of edges) { g[x].push([y, 1]); g[y].push([x, -1]); } const ans: number[] = Array(n).fill(0); const dfs = (i: number, fa: number) => { for (const [j, k] of g[i]) { if (j !== fa) { ans[0] += k < 0 ? 1 : 0; dfs(j, i); } } }; const dfs2 = (i: number, fa: number) => { for (const [j, k] of g[i]) { if (j !== fa) { ans[j] = ans[i] + k; dfs2(j, i); } } }; dfs(0, -1); dfs2(0, -1); return ans; }