Welcome to Subscribe On Youtube
2846. Minimum Edge Weight Equilibrium Queries in a Tree
Description
There is an undirected tree with n nodes labeled from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ui, vi, wi] indicates that there is an edge between nodes ui and vi with weight wi in the tree.
You are also given a 2D integer array queries of length m, where queries[i] = [ai, bi]. For each query, find the minimum number of operations required to make the weight of every edge on the path from ai to bi equal. In one operation, you can choose any edge of the tree and change its weight to any value.
Note that:
- Queries are independent of each other, meaning that the tree returns to its initial state on each new query.
- The path from
aitobiis a sequence of distinct nodes starting with nodeaiand ending with nodebisuch that every two adjacent nodes in the sequence share an edge in the tree.
Return an array answer of length m where answer[i] is the answer to the ith query.
Example 1:
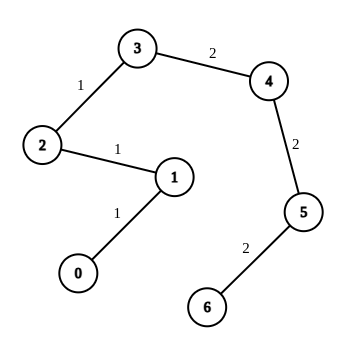
Input: n = 7, edges = [[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]], queries = [[0,3],[3,6],[2,6],[0,6]] Output: [0,0,1,3] Explanation: In the first query, all the edges in the path from 0 to 3 have a weight of 1. Hence, the answer is 0. In the second query, all the edges in the path from 3 to 6 have a weight of 2. Hence, the answer is 0. In the third query, we change the weight of edge [2,3] to 2. After this operation, all the edges in the path from 2 to 6 have a weight of 2. Hence, the answer is 1. In the fourth query, we change the weights of edges [0,1], [1,2] and [2,3] to 2. After these operations, all the edges in the path from 0 to 6 have a weight of 2. Hence, the answer is 3. For each queries[i], it can be shown that answer[i] is the minimum number of operations needed to equalize all the edge weights in the path from ai to bi.
Example 2:
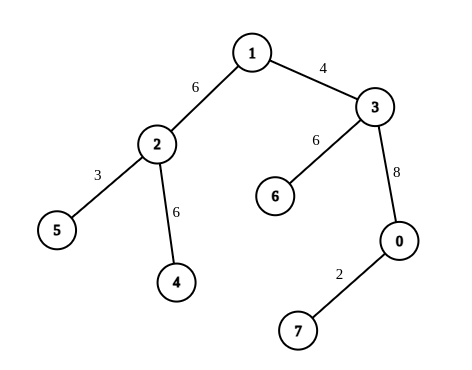
Input: n = 8, edges = [[1,2,6],[1,3,4],[2,4,6],[2,5,3],[3,6,6],[3,0,8],[7,0,2]], queries = [[4,6],[0,4],[6,5],[7,4]] Output: [1,2,2,3] Explanation: In the first query, we change the weight of edge [1,3] to 6. After this operation, all the edges in the path from 4 to 6 have a weight of 6. Hence, the answer is 1. In the second query, we change the weight of edges [0,3] and [3,1] to 6. After these operations, all the edges in the path from 0 to 4 have a weight of 6. Hence, the answer is 2. In the third query, we change the weight of edges [1,3] and [5,2] to 6. After these operations, all the edges in the path from 6 to 5 have a weight of 6. Hence, the answer is 2. In the fourth query, we change the weights of edges [0,7], [0,3] and [1,3] to 6. After these operations, all the edges in the path from 7 to 4 have a weight of 6. Hence, the answer is 3. For each queries[i], it can be shown that answer[i] is the minimum number of operations needed to equalize all the edge weights in the path from ai to bi.
Constraints:
1 <= n <= 104edges.length == n - 1edges[i].length == 30 <= ui, vi < n1 <= wi <= 26- The input is generated such that
edgesrepresents a valid tree. 1 <= queries.length == m <= 2 * 104queries[i].length == 20 <= ai, bi < n
Solutions
Solution 1: Binary Lifting for LCA
The problem asks for the minimum number of operations to make all edge weights the same on the path between any two points. This is essentially the length of the path between these two points, minus the number of times the most frequently occurring edge appears on the path.
The length of the path between two points can be obtained by finding the LCA (Lowest Common Ancestor) using binary lifting. Let’s denote the two points as $u$ and $v$, and their LCA as $x$. Then, the path length from $u$ to $v$ is $depth(u) + depth(v) - 2 \times depth(x)$.
Additionally, we can use an array $cnt[n][26]$ to record the number of occurrences of each edge weight from the root node to each node. Then, the number of times the most frequently occurring edge appears on the path from $u$ to $v$ is $\max_{0 \leq j < 26} cnt[u][j] + cnt[v][j] - 2 \times cnt[x][j]$, where $x$ is the LCA of $u$ and $v$.
The process of finding the LCA using binary lifting is as follows:
We denote the depth of each node as $depth$, its parent node as $p$, and $f[i][j]$ as the $2^j$th ancestor of node $i$. Then, for any two points $x$ and $y$, we can find their LCA as follows:
- If $depth(x) < depth(y)$, then swap $x$ and $y$, i.e., ensure that the depth of $x$ is not less than the depth of $y$;
- Next, we continuously raise the depth of $x$ until the depths of $x$ and $y$ are the same, at which point the depths of $x$ and $y$ are both $depth(x)$;
- Then, we raise the depths of $x$ and $y$ simultaneously until the parents of $x$ and $y$ are the same, at which point the parents of $x$ and $y$ are both $f[x][0]$, which is the LCA of $x$ and $y$.
Finally, the minimum number of operations from node $u$ to node $v$ is $depth(u) + depth(v) - 2 \times depth(x) - \max_{0 \leq j < 26} cnt[u][j] + cnt[v][j] - 2 \times cnt[x][j]$.
The time complexity is $O((n + q) \times C \times \log n)$, and the space complexity is $O(n \times C \times \log n)$. Here, $C$ is the maximum value of the edge weight.
-
class Solution { public int[] minOperationsQueries(int n, int[][] edges, int[][] queries) { int m = 32 - Integer.numberOfLeadingZeros(n); List<int[]>[] g = new List[n]; Arrays.setAll(g, i -> new ArrayList<>()); int[][] f = new int[n][m]; int[] p = new int[n]; int[][] cnt = new int[n][0]; int[] depth = new int[n]; for (var e : edges) { int u = e[0], v = e[1], w = e[2] - 1; g[u].add(new int[] {v, w}); g[v].add(new int[] {u, w}); } cnt[0] = new int[26]; Deque<Integer> q = new ArrayDeque<>(); q.offer(0); while (!q.isEmpty()) { int i = q.poll(); f[i][0] = p[i]; for (int j = 1; j < m; ++j) { f[i][j] = f[f[i][j - 1]][j - 1]; } for (var nxt : g[i]) { int j = nxt[0], w = nxt[1]; if (j != p[i]) { p[j] = i; cnt[j] = cnt[i].clone(); cnt[j][w]++; depth[j] = depth[i] + 1; q.offer(j); } } } int k = queries.length; int[] ans = new int[k]; for (int i = 0; i < k; ++i) { int u = queries[i][0], v = queries[i][1]; int x = u, y = v; if (depth[x] < depth[y]) { int t = x; x = y; y = t; } for (int j = m - 1; j >= 0; --j) { if (depth[x] - depth[y] >= (1 << j)) { x = f[x][j]; } } for (int j = m - 1; j >= 0; --j) { if (f[x][j] != f[y][j]) { x = f[x][j]; y = f[y][j]; } } if (x != y) { x = p[x]; } int mx = 0; for (int j = 0; j < 26; ++j) { mx = Math.max(mx, cnt[u][j] + cnt[v][j] - 2 * cnt[x][j]); } ans[i] = depth[u] + depth[v] - 2 * depth[x] - mx; } return ans; } } -
class Solution { public: vector<int> minOperationsQueries(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) { int m = 32 - __builtin_clz(n); vector<pair<int, int>> g[n]; int f[n][m]; int p[n]; int cnt[n][26]; int depth[n]; memset(f, 0, sizeof(f)); memset(cnt, 0, sizeof(cnt)); memset(depth, 0, sizeof(depth)); memset(p, 0, sizeof(p)); for (auto& e : edges) { int u = e[0], v = e[1], w = e[2] - 1; g[u].emplace_back(v, w); g[v].emplace_back(u, w); } queue<int> q; q.push(0); while (!q.empty()) { int i = q.front(); q.pop(); f[i][0] = p[i]; for (int j = 1; j < m; ++j) { f[i][j] = f[f[i][j - 1]][j - 1]; } for (auto& [j, w] : g[i]) { if (j != p[i]) { p[j] = i; memcpy(cnt[j], cnt[i], sizeof(cnt[i])); cnt[j][w]++; depth[j] = depth[i] + 1; q.push(j); } } } vector<int> ans; for (auto& qq : queries) { int u = qq[0], v = qq[1]; int x = u, y = v; if (depth[x] < depth[y]) { swap(x, y); } for (int j = m - 1; ~j; --j) { if (depth[x] - depth[y] >= (1 << j)) { x = f[x][j]; } } for (int j = m - 1; ~j; --j) { if (f[x][j] != f[y][j]) { x = f[x][j]; y = f[y][j]; } } if (x != y) { x = p[x]; } int mx = 0; for (int j = 0; j < 26; ++j) { mx = max(mx, cnt[u][j] + cnt[v][j] - 2 * cnt[x][j]); } ans.push_back(depth[u] + depth[v] - 2 * depth[x] - mx); } return ans; } }; -
class Solution: def minOperationsQueries( self, n: int, edges: List[List[int]], queries: List[List[int]] ) -> List[int]: m = n.bit_length() g = [[] for _ in range(n)] f = [[0] * m for _ in range(n)] p = [0] * n cnt = [None] * n depth = [0] * n for u, v, w in edges: g[u].append((v, w - 1)) g[v].append((u, w - 1)) cnt[0] = [0] * 26 q = deque([0]) while q: i = q.popleft() f[i][0] = p[i] for j in range(1, m): f[i][j] = f[f[i][j - 1]][j - 1] for j, w in g[i]: if j != p[i]: p[j] = i cnt[j] = cnt[i][:] cnt[j][w] += 1 depth[j] = depth[i] + 1 q.append(j) ans = [] for u, v in queries: x, y = u, v if depth[x] < depth[y]: x, y = y, x for j in reversed(range(m)): if depth[x] - depth[y] >= (1 << j): x = f[x][j] for j in reversed(range(m)): if f[x][j] != f[y][j]: x, y = f[x][j], f[y][j] if x != y: x = p[x] mx = max(cnt[u][j] + cnt[v][j] - 2 * cnt[x][j] for j in range(26)) ans.append(depth[u] + depth[v] - 2 * depth[x] - mx) return ans -
func minOperationsQueries(n int, edges [][]int, queries [][]int) []int { m := bits.Len(uint(n)) g := make([][][2]int, n) f := make([][]int, n) for i := range f { f[i] = make([]int, m) } p := make([]int, n) cnt := make([][26]int, n) cnt[0] = [26]int{} depth := make([]int, n) for _, e := range edges { u, v, w := e[0], e[1], e[2]-1 g[u] = append(g[u], [2]int{v, w}) g[v] = append(g[v], [2]int{u, w}) } q := []int{0} for len(q) > 0 { i := q[0] q = q[1:] f[i][0] = p[i] for j := 1; j < m; j++ { f[i][j] = f[f[i][j-1]][j-1] } for _, nxt := range g[i] { j, w := nxt[0], nxt[1] if j != p[i] { p[j] = i cnt[j] = [26]int{} for k := 0; k < 26; k++ { cnt[j][k] = cnt[i][k] } cnt[j][w]++ depth[j] = depth[i] + 1 q = append(q, j) } } } ans := make([]int, len(queries)) for i, qq := range queries { u, v := qq[0], qq[1] x, y := u, v if depth[x] < depth[y] { x, y = y, x } for j := m - 1; j >= 0; j-- { if depth[x]-depth[y] >= (1 << j) { x = f[x][j] } } for j := m - 1; j >= 0; j-- { if f[x][j] != f[y][j] { x, y = f[x][j], f[y][j] } } if x != y { x = p[x] } mx := 0 for j := 0; j < 26; j++ { mx = max(mx, cnt[u][j]+cnt[v][j]-2*cnt[x][j]) } ans[i] = depth[u] + depth[v] - 2*depth[x] - mx } return ans } func max(a, b int) int { if a > b { return a } return b }