2812. Find the Safest Path in a Grid

Description

You are given a 0-indexed 2D matrix grid of size n x n, where (r, c) represents:

A cell containing a thief if grid[r][c] = 1
An empty cell if grid[r][c] = 0

You are initially positioned at cell (0, 0). In one move, you can move to any adjacent cell in the grid, including cells containing thieves.

The safeness factor of a path on the grid is defined as the minimum manhattan distance from any cell in the path to any thief in the grid.

Return the maximum safeness factor of all paths leading to cell (n - 1, n - 1).

An adjacent cell of cell (r, c), is one of the cells (r, c + 1), (r, c - 1), (r + 1, c) and (r - 1, c) if it exists.

The Manhattan distance between two cells (a, b) and (x, y) is equal to |a - x| + |b - y|, where |val| denotes the absolute value of val.

Example 1:

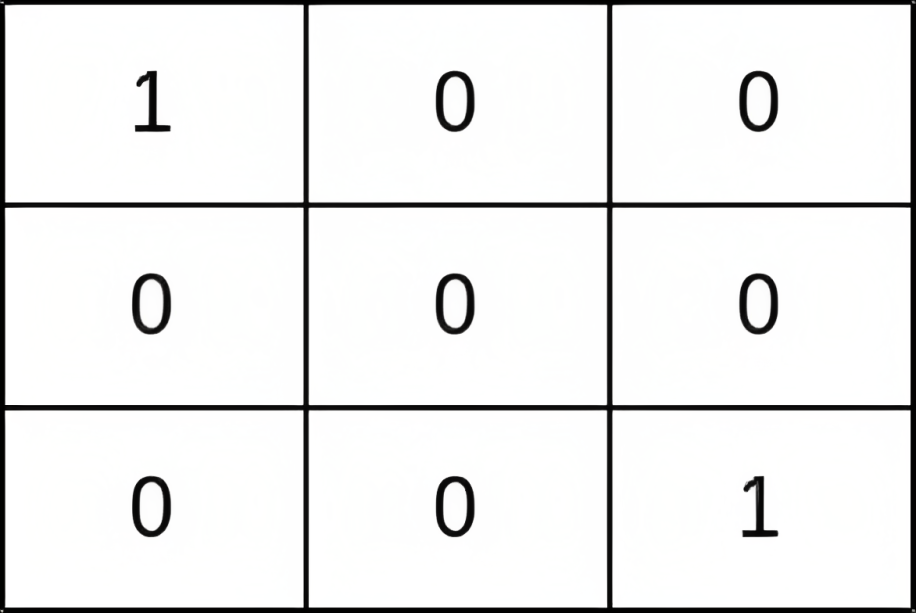
Input: grid = [[1,0,0],[0,0,0],[0,0,1]]
Output: 0
Explanation: All paths from (0, 0) to (n - 1, n - 1) go through the thieves in cells (0, 0) and (n - 1, n - 1).

Example 2:

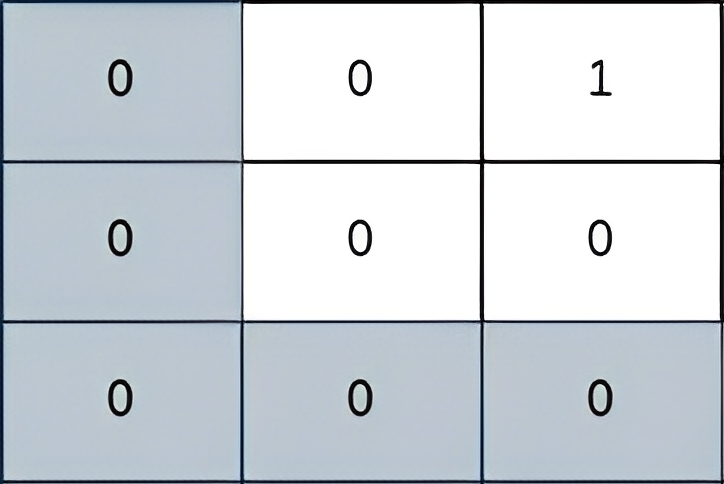
Input: grid = [[0,0,1],[0,0,0],[0,0,0]]
Output: 2
Explanation: The path depicted in the picture above has a safeness factor of 2 since:
- The closest cell of the path to the thief at cell (0, 2) is cell (0, 0). The distance between them is | 0 - 0 | + | 0 - 2 | = 2.
It can be shown that there are no other paths with a higher safeness factor.

Example 3:

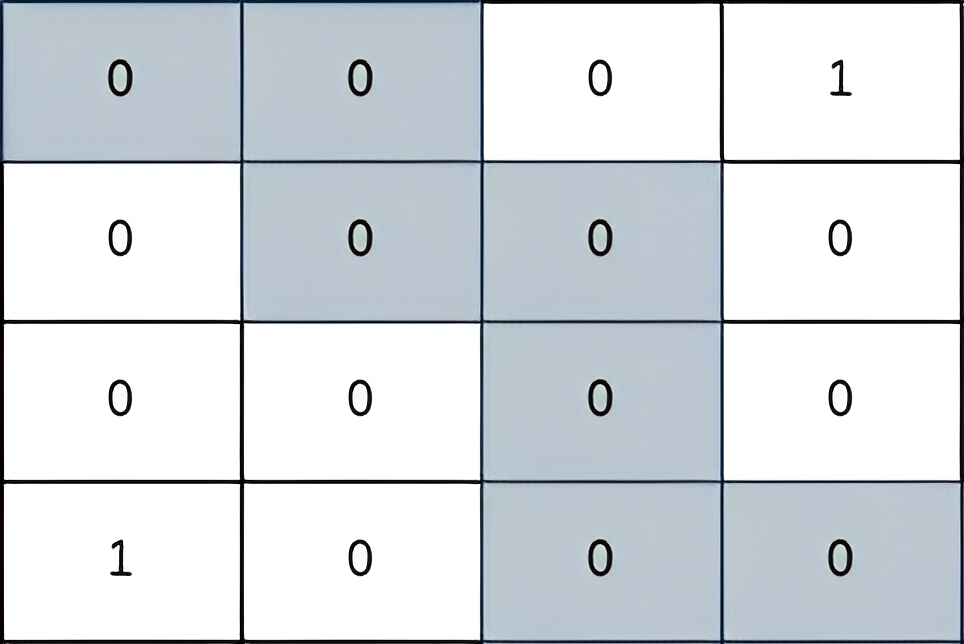
Input: grid = [[0,0,0,1],[0,0,0,0],[0,0,0,0],[1,0,0,0]]
Output: 2
Explanation: The path depicted in the picture above has a safeness factor of 2 since:
- The closest cell of the path to the thief at cell (0, 3) is cell (1, 2). The distance between them is | 0 - 1 | + | 3 - 2 | = 2.
- The closest cell of the path to the thief at cell (3, 0) is cell (3, 2). The distance between them is | 3 - 3 | + | 0 - 2 | = 2.
It can be shown that there are no other paths with a higher safeness factor.

Constraints:

1 <= grid.length == n <= 400
grid[i].length == n
grid[i][j] is either 0 or 1.
There is at least one thief in the grid.

Solutions

Solution 1: BFS + Sorting + Union-Find

We can first find out the positions of all thieves, and then start multi-source BFS from these positions to get the shortest distance from each position to the thieves. Then sort in descending order according to the distance, and add each position to the union-find set one by one. If the start and end points are in the same connected component, the current distance is the answer.

The time complexity is $O(n^2 \times \log n)$, and the space complexity $O(n^2)$. Where $n$ is the size of the grid.

class Solution {
    public int maximumSafenessFactor(List<List<Integer>> grid) {
        int n = grid.size();
        if (grid.get(0).get(0) == 1 || grid.get(n - 1).get(n - 1) == 1) {
            return 0;
        }
        Deque<int[]> q = new ArrayDeque<>();
        int[][] dist = new int[n][n];
        final int inf = 1 << 30;
        for (int[] d : dist) {
            Arrays.fill(d, inf);
        }
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid.get(i).get(j) == 1) {
                    dist[i][j] = 0;
                    q.offer(new int[] {i, j});
                }
            }
        }
        int[] dirs = {-1, 0, 1, 0, -1};
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int i = p[0], j = p[1];
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < n && y >= 0 && y < n && dist[x][y] == inf) {
                    dist[x][y] = dist[i][j] + 1;
                    q.offer(new int[] {x, y});
                }
            }
        }
        List<int[]> t = new ArrayList<>();
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                t.add(new int[] {dist[i][j], i, j});
            }
        }
        t.sort((a, b) -> Integer.compare(b[0], a[0]));
        UnionFind uf = new UnionFind(n * n);
        for (int[] p : t) {
            int d = p[0], i = p[1], j = p[2];
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < n && y >= 0 && y < n && dist[x][y] >= d) {
                    uf.union(i * n + j, x * n + y);
                }
            }
            if (uf.find(0) == uf.find(n * n - 1)) {
                return d;
            }
        }
        return 0;
    }
}

class UnionFind {
    public int[] p;
    public int n;

    public UnionFind(int n) {
        p = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
        this.n = n;
    }

    public boolean union(int a, int b) {
        int pa = find(a);
        int pb = find(b);
        if (pa == pb) {
            return false;
        }
        p[pa] = pb;
        --n;
        return true;
    }

    public int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

class UnionFind {
public:
    vector<int> p;
    int n;

    UnionFind(int _n)
        : n(_n)
        , p(_n) {
        iota(p.begin(), p.end(), 0);
    }

    bool unite(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa == pb) return false;
        p[pa] = pb;
        --n;
        return true;
    }

    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
};

class Solution {
public:
    int maximumSafenessFactor(vector<vector<int>>& grid) {
        int n = grid.size();
        if (grid[0][0] || grid[n - 1][n - 1]) {
            return 0;
        }
        queue<pair<int, int>> q;
        int dist[n][n];
        memset(dist, 0x3f, sizeof(dist));
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j]) {
                    dist[i][j] = 0;
                    q.emplace(i, j);
                }
            }
        }
        int dirs[5] = {-1, 0, 1, 0, -1};
        while (!q.empty()) {
            auto [i, j] = q.front();
            q.pop();
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < n && y >= 0 && y < n && dist[x][y] == 0x3f3f3f3f) {
                    dist[x][y] = dist[i][j] + 1;
                    q.emplace(x, y);
                }
            }
        }
        vector<tuple<int, int, int>> t;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                t.emplace_back(dist[i][j], i, j);
            }
        }
        sort(t.begin(), t.end());
        reverse(t.begin(), t.end());
        UnionFind uf(n * n);
        for (auto [d, i, j] : t) {
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < n && y >= 0 && y < n && dist[x][y] >= d) {
                    uf.unite(i * n + j, x * n + y);
                }
            }
            if (uf.find(0) == uf.find(n * n - 1)) {
                return d;
            }
        }
        return 0;
    }
};

class UnionFind:
    def __init__(self, n):
        self.p = list(range(n))
        self.size = [1] * n

    def find(self, x):
        if self.p[x] != x:
            self.p[x] = self.find(self.p[x])
        return self.p[x]

    def union(self, a, b):
        pa, pb = self.find(a), self.find(b)
        if pa == pb:
            return False
        if self.size[pa] > self.size[pb]:
            self.p[pb] = pa
            self.size[pa] += self.size[pb]
        else:
            self.p[pa] = pb
            self.size[pb] += self.size[pa]
        return True


class Solution:
    def maximumSafenessFactor(self, grid: List[List[int]]) -> int:
        n = len(grid)
        if grid[0][0] or grid[n - 1][n - 1]:
            return 0
        q = deque()
        dist = [[inf] * n for _ in range(n)]
        for i in range(n):
            for j in range(n):
                if grid[i][j]:
                    q.append((i, j))
                    dist[i][j] = 0
        dirs = (-1, 0, 1, 0, -1)
        while q:
            i, j = q.popleft()
            for a, b in pairwise(dirs):
                x, y = i + a, j + b
                if 0 <= x < n and 0 <= y < n and dist[x][y] == inf:
                    dist[x][y] = dist[i][j] + 1
                    q.append((x, y))

        q = ((dist[i][j], i, j) for i in range(n) for j in range(n))
        q = sorted(q, reverse=True)
        uf = UnionFind(n * n)
        for d, i, j in q:
            for a, b in pairwise(dirs):
                x, y = i + a, j + b
                if 0 <= x < n and 0 <= y < n and dist[x][y] >= d:
                    uf.union(i * n + j, x * n + y)
            if uf.find(0) == uf.find(n * n - 1):
                return int(d)
        return 0

type unionFind struct {
	p []int
	n int
}

func newUnionFind(n int) *unionFind {
	p := make([]int, n)
	for i := range p {
		p[i] = i
	}
	return &unionFind{p, n}
}

func (uf *unionFind) find(x int) int {
	if uf.p[x] != x {
		uf.p[x] = uf.find(uf.p[x])
	}
	return uf.p[x]
}

func (uf *unionFind) union(a, b int) bool {
	if uf.find(a) == uf.find(b) {
		return false
	}
	uf.p[uf.find(a)] = uf.find(b)
	uf.n--
	return true
}

func maximumSafenessFactor(grid [][]int) int {
	n := len(grid)
	if grid[0][0] == 1 || grid[n-1][n-1] == 1 {
		return 0
	}
	q := [][2]int{}
	dist := make([][]int, n)
	const inf = 1 << 30
	for i := range dist {
		dist[i] = make([]int, n)
		for j := range dist[i] {
			dist[i][j] = inf
		}
	}
	for i := 0; i < n; i++ {
		for j := 0; j < n; j++ {
			if grid[i][j] == 1 {
				dist[i][j] = 0
				q = append(q, [2]int{i, j})
			}
		}
	}
	dirs := [5]int{-1, 0, 1, 0, -1}
	for len(q) > 0 {
		p := q[0]
		q = q[1:]
		i, j := p[0], p[1]
		for k := 0; k < 4; k++ {
			x, y := i+dirs[k], j+dirs[k+1]
			if x >= 0 && x < n && y >= 0 && y < n && dist[x][y] == inf {
				dist[x][y] = dist[i][j] + 1
				q = append(q, [2]int{x, y})
			}
		}
	}
	t := [][3]int{}
	for i := 0; i < n; i++ {
		for j := 0; j < n; j++ {
			t = append(t, [3]int{dist[i][j], i, j})
		}
	}
	sort.Slice(t, func(i, j int) bool {
		return t[i][0] > t[j][0]
	})
	uf := newUnionFind(n * n)
	for _, p := range t {
		d, i, j := p[0], p[1], p[2]
		for k := 0; k < 4; k++ {
			x, y := i+dirs[k], j+dirs[k+1]
			if x >= 0 && x < n && y >= 0 && y < n && dist[x][y] >= d {
				uf.union(i*n+j, x*n+y)
			}
		}
		if uf.find(0) == uf.find(n*n-1) {
			return d
		}
	}
	return 0
}

class UnionFind {
    private p: number[];
    private n: number;

    constructor(n: number) {
        this.n = n;
        this.p = Array(n)
            .fill(0)
            .map((_, i) => i);
    }

    find(x: number): number {
        if (this.p[x] !== x) {
            this.p[x] = this.find(this.p[x]);
        }
        return this.p[x];
    }

    union(a: number, b: number): boolean {
        const pa = this.find(a);
        const pb = this.find(b);
        if (pa !== pb) {
            this.p[pa] = pb;
            this.n--;
            return true;
        }
        return false;
    }
}

function maximumSafenessFactor(grid: number[][]): number {
    const n = grid.length;
    if (grid[0][0] === 1 || grid[n - 1][n - 1] === 1) {
        return 0;
    }
    const q: number[][] = [];
    const inf = 1 << 30;
    const dist: number[][] = Array(n)
        .fill(0)
        .map(() => Array(n).fill(inf));
    for (let i = 0; i < n; ++i) {
        for (let j = 0; j < n; ++j) {
            if (grid[i][j] === 1) {
                dist[i][j] = 0;
                q.push([i, j]);
            }
        }
    }
    const dirs = [-1, 0, 1, 0, -1];
    while (q.length) {
        const [i, j] = q.shift()!;
        for (let k = 0; k < 4; ++k) {
            const [x, y] = [i + dirs[k], j + dirs[k + 1]];
            if (x >= 0 && x < n && y >= 0 && y < n && dist[x][y] === inf) {
                dist[x][y] = dist[i][j] + 1;
                q.push([x, y]);
            }
        }
    }
    const t: number[][] = [];
    for (let i = 0; i < n; ++i) {
        for (let j = 0; j < n; ++j) {
            t.push([dist[i][j], i, j]);
        }
    }
    t.sort((a, b) => b[0] - a[0]);
    const uf = new UnionFind(n * n);
    for (const [d, i, j] of t) {
        for (let k = 0; k < 4; ++k) {
            const [x, y] = [i + dirs[k], j + dirs[k + 1]];
            if (x >= 0 && x < n && y >= 0 && y < n && dist[x][y] >= d) {
                uf.union(i * n + j, x * n + y);
            }
        }
        if (uf.find(0) == uf.find(n * n - 1)) {
            return d;
        }
    }
    return 0;
}

use std::collections::VecDeque;
impl Solution {
    fn dfs(i: usize, j: usize, v: i32, g: &Vec<Vec<i32>>, vis: &mut Vec<Vec<bool>>) -> bool {
        if vis[i][j] || g[i][j] <= v {
            return false;
        }
        vis[i][j] = true;
        let n = g.len();
        (i == n - 1 && j == n - 1) ||
            (i != 0 && Self::dfs(i - 1, j, v, g, vis)) ||
            (i != n - 1 && Self::dfs(i + 1, j, v, g, vis)) ||
            (j != 0 && Self::dfs(i, j - 1, v, g, vis)) ||
            (j != n - 1 && Self::dfs(i, j + 1, v, g, vis))
    }

    pub fn maximum_safeness_factor(grid: Vec<Vec<i32>>) -> i32 {
        let n = grid.len();
        let mut g = vec![vec![-1; n]; n];
        let mut q = VecDeque::new();
        for i in 0..n {
            for j in 0..n {
                if grid[i][j] == 1 {
                    q.push_back((i, j));
                }
            }
        }
        let mut level = 0;
        while !q.is_empty() {
            let m = q.len();
            for _ in 0..m {
                let (i, j) = q.pop_front().unwrap();
                if g[i][j] != -1 {
                    continue;
                }
                g[i][j] = level;
                if i != n - 1 {
                    q.push_back((i + 1, j));
                }
                if i != 0 {
                    q.push_back((i - 1, j));
                }
                if j != n - 1 {
                    q.push_back((i, j + 1));
                }
                if j != 0 {
                    q.push_back((i, j - 1));
                }
            }
            level += 1;
        }
        let mut left = 0;
        let mut right = level;
        while left < right {
            let mid = (left + right) >> 1;
            if Self::dfs(0, 0, mid, &g, &mut vec![vec![false; n]; n]) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        right
    }
}

2812 - Find the Safest Path in a Grid

2812. Find the Safest Path in a Grid

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

2812. Find the Safest Path in a Grid

Description

Solutions

All Problems

All Solutions