Welcome to Subscribe On Youtube
2807. Insert Greatest Common Divisors in Linked List
Description
Given the head of a linked list head, in which each node contains an integer value.
Between every pair of adjacent nodes, insert a new node with a value equal to the greatest common divisor of them.
Return the linked list after insertion.
The greatest common divisor of two numbers is the largest positive integer that evenly divides both numbers.
Example 1:
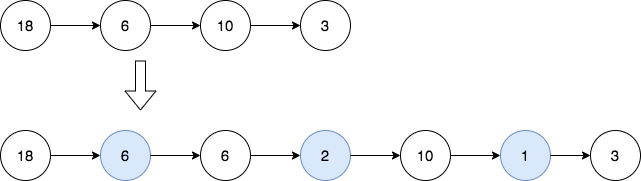
Input: head = [18,6,10,3] Output: [18,6,6,2,10,1,3] Explanation: The 1st diagram denotes the initial linked list and the 2nd diagram denotes the linked list after inserting the new nodes (nodes in blue are the inserted nodes). - We insert the greatest common divisor of 18 and 6 = 6 between the 1st and the 2nd nodes. - We insert the greatest common divisor of 6 and 10 = 2 between the 2nd and the 3rd nodes. - We insert the greatest common divisor of 10 and 3 = 1 between the 3rd and the 4th nodes. There are no more adjacent nodes, so we return the linked list.
Example 2:
Input: head = [7] Output: [7] Explanation: The 1st diagram denotes the initial linked list and the 2nd diagram denotes the linked list after inserting the new nodes. There are no pairs of adjacent nodes, so we return the initial linked list.
Constraints:
- The number of nodes in the list is in the range
[1, 5000]. 1 <= Node.val <= 1000
Solutions
Solution 1: Simulation
We use two pointers $pre$ and $cur$ to point to the current node and the next node respectively. We only need to insert a new node between $pre$ and $cur$. Therefore, each time we calculate the greatest common divisor $x$ of $pre$ and $cur$, we insert a new node with value $x$ between $pre$ and $cur$. Then we update $pre = cur$ and $cur = cur.next$, and continue to traverse the linked list until $cur$ is null.
The time complexity is $O(n \times \log M)$, where $n$ is the length of the linked list, and $M$ is the maximum value of the nodes in the linked list. Ignoring the space consumption of the result linked list, the space complexity is $O(1)$.
-
/** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode() {} * ListNode(int val) { this.val = val; } * ListNode(int val, ListNode next) { this.val = val; this.next = next; } * } */ class Solution { public ListNode insertGreatestCommonDivisors(ListNode head) { for (ListNode pre = head, cur = head.next; cur != null; cur = cur.next) { int x = gcd(pre.val, cur.val); pre.next = new ListNode(x, cur); pre = cur; } return head; } private int gcd(int a, int b) { if (b == 0) { return a; } return gcd(b, a % b); } } -
/** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode() : val(0), next(nullptr) {} * ListNode(int x) : val(x), next(nullptr) {} * ListNode(int x, ListNode *next) : val(x), next(next) {} * }; */ class Solution { public: ListNode* insertGreatestCommonDivisors(ListNode* head) { ListNode* pre = head; for (ListNode* cur = head->next; cur; cur = cur->next) { int x = gcd(pre->val, cur->val); pre->next = new ListNode(x, cur); pre = cur; } return head; } }; -
# Definition for singly-linked list. # class ListNode: # def __init__(self, val=0, next=None): # self.val = val # self.next = next class Solution: def insertGreatestCommonDivisors( self, head: Optional[ListNode] ) -> Optional[ListNode]: pre, cur = head, head.next while cur: x = gcd(pre.val, cur.val) pre.next = ListNode(x, cur) pre, cur = cur, cur.next return head -
/** * Definition for singly-linked list. * type ListNode struct { * Val int * Next *ListNode * } */ func insertGreatestCommonDivisors(head *ListNode) *ListNode { for pre, cur := head, head.Next; cur != nil; cur = cur.Next { x := gcd(pre.Val, cur.Val) pre.Next = &ListNode{x, cur} pre = cur } return head } func gcd(a, b int) int { if b == 0 { return a } return gcd(b, a%b) } -
/** * Definition for singly-linked list. * class ListNode { * val: number * next: ListNode | null * constructor(val?: number, next?: ListNode | null) { * this.val = (val===undefined ? 0 : val) * this.next = (next===undefined ? null : next) * } * } */ function insertGreatestCommonDivisors(head: ListNode | null): ListNode | null { for (let pre = head, cur = head.next; cur; cur = cur.next) { const x = gcd(pre.val, cur.val); pre.next = new ListNode(x, cur); pre = cur; } return head; } function gcd(a: number, b: number): number { if (b === 0) { return a; } return gcd(b, a % b); }