Welcome to Subscribe On Youtube
2673. Make Costs of Paths Equal in a Binary Tree
Description
You are given an integer n representing the number of nodes in a perfect binary tree consisting of nodes numbered from 1 to n. The root of the tree is node 1 and each node i in the tree has two children where the left child is the node 2 * i and the right child is 2 * i + 1.
Each node in the tree also has a cost represented by a given 0-indexed integer array cost of size n where cost[i] is the cost of node i + 1. You are allowed to increment the cost of any node by 1 any number of times.
Return the minimum number of increments you need to make the cost of paths from the root to each leaf node equal.
Note:
- A perfect binary tree is a tree where each node, except the leaf nodes, has exactly 2 children.
- The cost of a path is the sum of costs of nodes in the path.
Example 1:
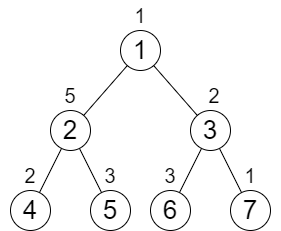
Input: n = 7, cost = [1,5,2,2,3,3,1] Output: 6 Explanation: We can do the following increments: - Increase the cost of node 4 one time. - Increase the cost of node 3 three times. - Increase the cost of node 7 two times. Each path from the root to a leaf will have a total cost of 9. The total increments we did is 1 + 3 + 2 = 6. It can be shown that this is the minimum answer we can achieve.
Example 2:
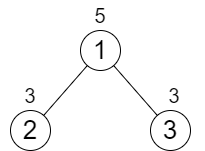
Input: n = 3, cost = [5,3,3] Output: 0 Explanation: The two paths already have equal total costs, so no increments are needed.
Constraints:
3 <= n <= 105n + 1is a power of2cost.length == n1 <= cost[i] <= 104
Solutions
-
class Solution { private int[] cost; private int n; private int ans; public int minIncrements(int n, int[] cost) { this.n = n; this.cost = cost; dfs(1); return ans; } private int dfs(int i) { if ((i << 1) > n) { return cost[i - 1]; } int l = dfs(i << 1); int r = dfs(i << 1 | 1); ans += Math.max(l, r) - Math.min(l, r); return cost[i - 1] + Math.max(l, r); } } -
class Solution { public: int minIncrements(int n, vector<int>& cost) { int ans = 0; function<int(int)> dfs = [&](int i) -> int { if ((i << 1) > n) { return cost[i - 1]; } int l = dfs(i << 1); int r = dfs(i << 1 | 1); ans += max(l, r) - min(l, r); return cost[i - 1] + max(l, r); }; dfs(1); return ans; } }; -
class Solution: def minIncrements(self, n: int, cost: List[int]) -> int: def dfs(i: int) -> int: if (i << 1) > n: return cost[i - 1] l, r = dfs(i << 1), dfs(i << 1 | 1) nonlocal ans ans += max(l, r) - min(l, r) return cost[i - 1] + max(l, r) ans = 0 dfs(1) return ans -
func minIncrements(n int, cost []int) (ans int) { var dfs func(int) int dfs = func(i int) int { if (i << 1) > n { return cost[i-1] } l, r := dfs(i<<1), dfs(i<<1|1) ans += max(l, r) - min(l, r) return cost[i-1] + max(l, r) } dfs(1) return ans } func max(a, b int) int { if a > b { return a } return b } func min(a, b int) int { if a < b { return a } return b } -
function minIncrements(n: number, cost: number[]): number { let ans = 0; const dfs = (i: number): number => { if (i << 1 > n) { return cost[i - 1]; } const [a, b] = [dfs(i << 1), dfs((i << 1) | 1)]; ans += Math.max(a, b) - Math.min(a, b); return cost[i - 1] + Math.max(a, b); }; dfs(1); return ans; }