Welcome to Subscribe On Youtube

2661. First Completely Painted Row or Column

Description

You are given a 0-indexed integer array arr, and an m x n integer matrix mat. arr and mat both contain all the integers in the range [1, m * n].

Go through each index i in arr starting from index 0 and paint the cell in mat containing the integer arr[i].

Return the smallest index i at which either a row or a column will be completely painted in mat.

 

Example 1:

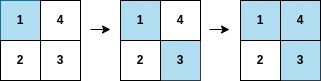
Input: arr = [1,3,4,2], mat = [[1,4],[2,3]]
Output: 2
Explanation: The moves are shown in order, and both the first row and second column of the matrix become fully painted at arr[2].

Example 2:

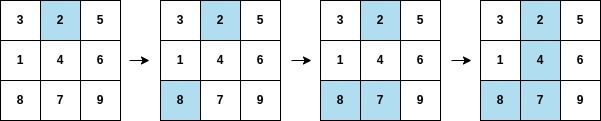
Input: arr = [2,8,7,4,1,3,5,6,9], mat = [[3,2,5],[1,4,6],[8,7,9]]
Output: 3
Explanation: The second column becomes fully painted at arr[3].

 

Constraints:

• m == mat.length
• n = mat[i].length
• arr.length == m * n
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 1 <= arr[i], mat[r][c] <= m * n
• All the integers of arr are unique.
• All the integers of mat are unique.

Solutions

Solution 1: Hash Table + Array Counting

We use a hash table $idx$ to record the position of each element in the matrix $mat$, that is $idx[mat[i][j]] = (i, j)$, and define two arrays $row$ and $col$ to record the number of colored elements in each row and each column respectively.

Traverse the array $arr$. For each element $arr[k]$, we find its position $(i, j)$ in the matrix $mat$, and then add $row[i]$ and $col[j]$ by one. If $row[i] = n$ or $col[j] = m$, it means that the $i$-th row or the $j$-th column has been colored, so $arr[k]$ is the element we are looking for, and we return $k$.

The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$. Here $m$ and $n$ are the number of rows and columns of the matrix $mat$ respectively.

• Java
• C++
• Python
• Go
• TypeScript
• RenderScript

• class Solution {
      public int firstCompleteIndex(int[] arr, int[][] mat) {
          int m = mat.length, n = mat[0].length;
          Map<Integer, int[]> idx = new HashMap<>();
          for (int i = 0; i < m; ++i) {
              for (int j = 0; j < n; ++j) {
                  idx.put(mat[i][j], new int[] {i, j});
              }
          }
          int[] row = new int[m];
          int[] col = new int[n];
          for (int k = 0;; ++k) {
              var x = idx.get(arr[k]);
              int i = x[0], j = x[1];
              ++row[i];
              ++col[j];
              if (row[i] == n || col[j] == m) {
                  return k;
              }
          }
      }
  }
  

• class Solution {
  public:
      int firstCompleteIndex(vector<int>& arr, vector<vector<int>>& mat) {
          int m = mat.size(), n = mat[0].size();
          unordered_map<int, pair<int, int>> idx;
          for (int i = 0; i < m; ++i) {
              for (int j = 0; j < n; ++j) {
                  idx[mat[i][j]] = {i, j};
              }
          }
          vector<int> row(m), col(n);
          for (int k = 0;; ++k) {
              auto [i, j] = idx[arr[k]];
              ++row[i];
              ++col[j];
              if (row[i] == n || col[j] == m) {
                  return k;
              }
          }
      }
  };
  

• class Solution:
      def firstCompleteIndex(self, arr: List[int], mat: List[List[int]]) -> int:
          m, n = len(mat), len(mat[0])
          idx = {}
          for i in range(m):
              for j in range(n):
                  idx[mat[i][j]] = (i, j)
          row = [0] * m
          col = [0] * n
          for k in range(len(arr)):
              i, j = idx[arr[k]]
              row[i] += 1
              col[j] += 1
              if row[i] == n or col[j] == m:
                  return k
  
  

• func firstCompleteIndex(arr []int, mat [][]int) int {
  	m, n := len(mat), len(mat[0])
  	idx := map[int][2]int{}
  	for i := range mat {
  		for j := range mat[i] {
  			idx[mat[i][j]] = [2]int{i, j}
  		}
  	}
  	row := make([]int, m)
  	col := make([]int, n)
  	for k := 0; ; k++ {
  		x := idx[arr[k]]
  		i, j := x[0], x[1]
  		row[i]++
  		col[j]++
  		if row[i] == n || col[j] == m {
  			return k
  		}
  	}
  }
  

• function firstCompleteIndex(arr: number[], mat: number[][]): number {
      const m = mat.length;
      const n = mat[0].length;
      const idx: Map<number, number[]> = new Map();
      for (let i = 0; i < m; ++i) {
          for (let j = 0; j < n; ++j) {
              idx.set(mat[i][j], [i, j]);
          }
      }
      const row: number[] = new Array(m).fill(0);
      const col: number[] = new Array(n).fill(0);
      for (let k = 0; ; ++k) {
          const [i, j] = idx.get(arr[k])!;
          ++row[i];
          ++col[j];
          if (row[i] === n || col[j] === m) {
              return k;
          }
      }
  }
  
  

• use std::collections::HashMap;
  
  impl Solution {
      pub fn first_complete_index(arr: Vec<i32>, mat: Vec<Vec<i32>>) -> i32 {
          let m = mat.len();
          let n = mat[0].len();
          let mut idx = HashMap::new();
          for i in 0..m {
              for j in 0..n {
                  idx.insert(mat[i][j], [i, j]);
              }
          }
  
          let mut row = vec![0; m];
          let mut col = vec![0; n];
          for k in 0..arr.len() {
              let x = idx.get(&arr[k]).unwrap();
              let i = x[0];
              let j = x[1];
              row[i] += 1;
              col[j] += 1;
              if row[i] == n || col[j] == m {
                  return k as i32;
              }
          }
  
          -1
      }
  }
  
  

All Problems

All Solutions