Welcome to Subscribe On Youtube
2737. Find the Closest Marked Node
Description
You are given a positive integer n which is the number of nodes of a 0-indexed directed weighted graph and a 0-indexed 2D array edges where edges[i] = [ui, vi, wi] indicates that there is an edge from node ui to node vi with weight wi.
You are also given a node s and a node array marked; your task is to find the minimum distance from s to any of the nodes in marked.
Return an integer denoting the minimum distance from s to any node in marked or -1 if there are no paths from s to any of the marked nodes.
Example 1:
Input: n = 4, edges = [[0,1,1],[1,2,3],[2,3,2],[0,3,4]], s = 0, marked = [2,3] Output: 4 Explanation: There is one path from node 0 (the green node) to node 2 (a red node), which is 0->1->2, and has a distance of 1 + 3 = 4. There are two paths from node 0 to node 3 (a red node), which are 0->1->2->3 and 0->3, the first one has a distance of 1 + 3 + 2 = 6 and the second one has a distance of 4. The minimum of them is 4.
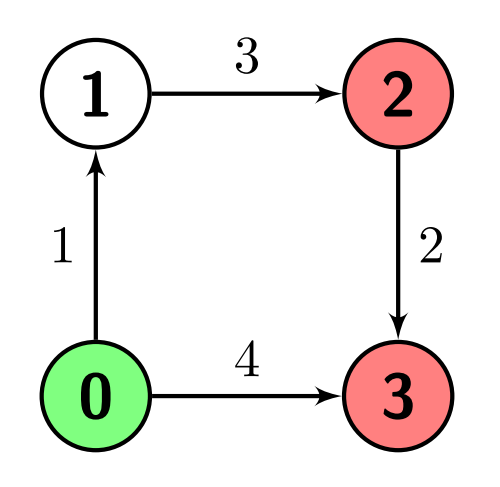
Example 2:
Input: n = 5, edges = [[0,1,2],[0,2,4],[1,3,1],[2,3,3],[3,4,2]], s = 1, marked = [0,4] Output: 3 Explanation: There are no paths from node 1 (the green node) to node 0 (a red node). There is one path from node 1 to node 4 (a red node), which is 1->3->4, and has a distance of 1 + 2 = 3. So the answer is 3.
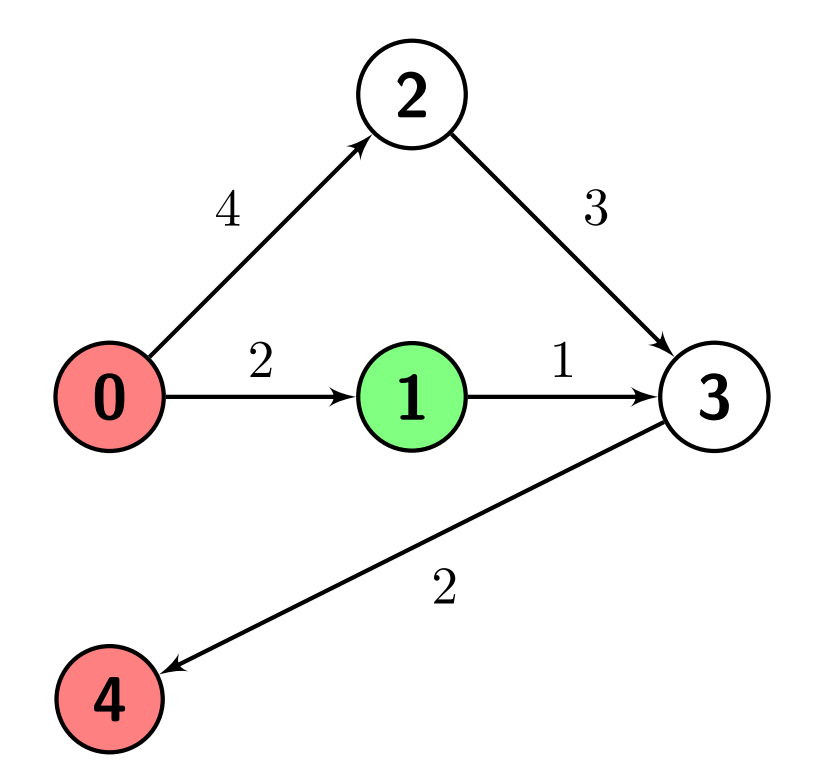
Example 3:
Input: n = 4, edges = [[0,1,1],[1,2,3],[2,3,2]], s = 3, marked = [0,1] Output: -1 Explanation: There are no paths from node 3 (the green node) to any of the marked nodes (the red nodes), so the answer is -1.

Constraints:
2 <= n <= 5001 <= edges.length <= 104edges[i].length = 30 <= edges[i][0], edges[i][1] <= n - 11 <= edges[i][2] <= 1061 <= marked.length <= n - 10 <= s, marked[i] <= n - 1s != marked[i]marked[i] != marked[j]for everyi != j- The graph might have repeated edges.
- The graph is generated such that it has no self-loops.
Solutions
-
class Solution { public int minimumDistance(int n, List<List<Integer>> edges, int s, int[] marked) { final int inf = 1 << 29; int[][] g = new int[n][n]; for (var e : g) { Arrays.fill(e, inf); } for (var e : edges) { int u = e.get(0), v = e.get(1), w = e.get(2); g[u][v] = Math.min(g[u][v], w); } int[] dist = new int[n]; Arrays.fill(dist, inf); dist[s] = 0; boolean[] vis = new boolean[n]; for (int i = 0; i < n; ++i) { int t = -1; for (int j = 0; j < n; ++j) { if (!vis[j] && (t == -1 || dist[t] > dist[j])) { t = j; } } vis[t] = true; for (int j = 0; j < n; ++j) { dist[j] = Math.min(dist[j], dist[t] + g[t][j]); } } int ans = inf; for (int i : marked) { ans = Math.min(ans, dist[i]); } return ans >= inf ? -1 : ans; } } -
class Solution { public: int minimumDistance(int n, vector<vector<int>>& edges, int s, vector<int>& marked) { const int inf = 1 << 29; vector<vector<int>> g(n, vector<int>(n, inf)); vector<int> dist(n, inf); dist[s] = 0; vector<bool> vis(n); for (auto& e : edges) { int u = e[0], v = e[1], w = e[2]; g[u][v] = min(g[u][v], w); } for (int i = 0; i < n; ++i) { int t = -1; for (int j = 0; j < n; ++j) { if (!vis[j] && (t == -1 || dist[t] > dist[j])) { t = j; } } vis[t] = true; for (int j = 0; j < n; ++j) { dist[j] = min(dist[j], dist[t] + g[t][j]); } } int ans = inf; for (int i : marked) { ans = min(ans, dist[i]); } return ans >= inf ? -1 : ans; } }; -
class Solution: def minimumDistance( self, n: int, edges: List[List[int]], s: int, marked: List[int] ) -> int: g = [[inf] * n for _ in range(n)] for u, v, w in edges: g[u][v] = min(g[u][v], w) dist = [inf] * n vis = [False] * n dist[s] = 0 for _ in range(n): t = -1 for j in range(n): if not vis[j] and (t == -1 or dist[t] > dist[j]): t = j vis[t] = True for j in range(n): dist[j] = min(dist[j], dist[t] + g[t][j]) ans = min(dist[i] for i in marked) return -1 if ans >= inf else ans -
func minimumDistance(n int, edges [][]int, s int, marked []int) int { const inf = 1 << 29 g := make([][]int, n) dist := make([]int, n) for i := range g { g[i] = make([]int, n) for j := range g[i] { g[i][j] = inf } dist[i] = inf } dist[s] = 0 for _, e := range edges { u, v, w := e[0], e[1], e[2] g[u][v] = min(g[u][v], w) } vis := make([]bool, n) for _ = range g { t := -1 for j := 0; j < n; j++ { if !vis[j] && (t == -1 || dist[j] < dist[t]) { t = j } } vis[t] = true for j := 0; j < n; j++ { dist[j] = min(dist[j], dist[t]+g[t][j]) } } ans := inf for _, i := range marked { ans = min(ans, dist[i]) } if ans >= inf { return -1 } return ans } -
function minimumDistance(n: number, edges: number[][], s: number, marked: number[]): number { const inf = 1 << 29; const g: number[][] = Array(n) .fill(0) .map(() => Array(n).fill(inf)); const dist: number[] = Array(n).fill(inf); const vis: boolean[] = Array(n).fill(false); for (const [u, v, w] of edges) { g[u][v] = Math.min(g[u][v], w); } dist[s] = 0; for (let i = 0; i < n; ++i) { let t = -1; for (let j = 0; j < n; ++j) { if (!vis[j] && (t == -1 || dist[t] > dist[j])) { t = j; } } vis[t] = true; for (let j = 0; j < n; ++j) { dist[j] = Math.min(dist[j], dist[t] + g[t][j]); } } let ans = inf; for (const i of marked) { ans = Math.min(ans, dist[i]); } return ans >= inf ? -1 : ans; }