Welcome to Subscribe On Youtube
2647. Color the Triangle Red
Description
You are given an integer n. Consider an equilateral triangle of side length n, broken up into n2 unit equilateral triangles. The triangle has n 1-indexed rows where the ith row has 2i - 1 unit equilateral triangles.
The triangles in the ith row are also 1-indexed with coordinates from (i, 1) to (i, 2i - 1). The following image shows a triangle of side length 4 with the indexing of its triangle.
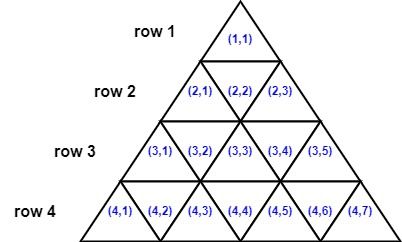
Two triangles are neighbors if they share a side. For example:
- Triangles
(1,1)and(2,2)are neighbors - Triangles
(3,2)and(3,3)are neighbors. - Triangles
(2,2)and(3,3)are not neighbors because they do not share any side.
Initially, all the unit triangles are white. You want to choose k triangles and color them red. We will then run the following algorithm:
- Choose a white triangle that has at least two red neighbors.
- If there is no such triangle, stop the algorithm.
- Color that triangle red.
- Go to step 1.
Choose the minimum k possible and set k triangles red before running this algorithm such that after the algorithm stops, all unit triangles are colored red.
Return a 2D list of the coordinates of the triangles that you will color red initially. The answer has to be of the smallest size possible. If there are multiple valid solutions, return any.
Example 1:
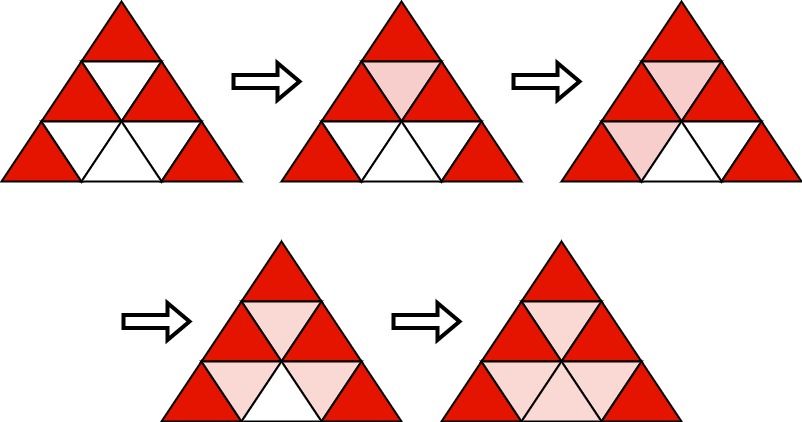
Input: n = 3 Output: [[1,1],[2,1],[2,3],[3,1],[3,5]] Explanation: Initially, we choose the shown 5 triangles to be red. Then, we run the algorithm: - Choose (2,2) that has three red neighbors and color it red. - Choose (3,2) that has two red neighbors and color it red. - Choose (3,4) that has three red neighbors and color it red. - Choose (3,3) that has three red neighbors and color it red. It can be shown that choosing any 4 triangles and running the algorithm will not make all triangles red.
Example 2:
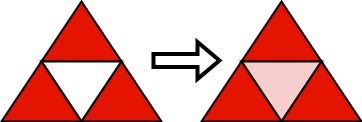
Input: n = 2 Output: [[1,1],[2,1],[2,3]] Explanation: Initially, we choose the shown 3 triangles to be red. Then, we run the algorithm: - Choose (2,2) that has three red neighbors and color it red. It can be shown that choosing any 2 triangles and running the algorithm will not make all triangles red.
Constraints:
1 <= n <= 1000
Solutions
Solution 1: Find the Pattern
We draw a graph to observe, and we can find that the first row only has one triangle and must be colored, and from the last row to the second row, the coloring scheme of every four rows is the same:
- The last row is colored at $(n, 1)$, $(n, 3)$, …, $(n, 2n - 1)$.
- The $n - 1$ row is colored at $(n - 1, 2)$.
- The $n - 2$ row is colored at $(n - 2, 3)$, $(n - 2, 5)$, …, $(n - 2, 2n - 5)$.
- The $n - 3$ row is colored at $(n - 3, 1)$.
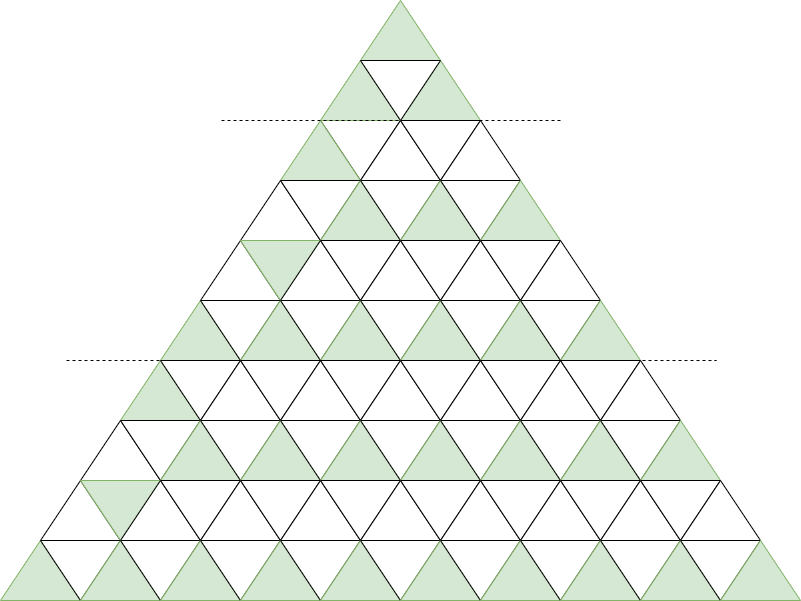
Therefore, we can color the first row according to the above rules, and then start from the last row, and color every four rows once until the second row ends.

The time complexity is $(n^2)$, where $n$ is the parameter given in the problem. Ignoring the space consumption of the answer array, the space complexity is $O(1)$.
-
class Solution { public int[][] colorRed(int n) { List<int[]> ans = new ArrayList<>(); ans.add(new int[] {1, 1}); for (int i = n, k = 0; i > 1; --i, k = (k + 1) % 4) { if (k == 0) { for (int j = 1; j < i << 1; j += 2) { ans.add(new int[] {i, j}); } } else if (k == 1) { ans.add(new int[] {i, 2}); } else if (k == 2) { for (int j = 3; j < i << 1; j += 2) { ans.add(new int[] {i, j}); } } else { ans.add(new int[] {i, 1}); } } return ans.toArray(new int[0][]); } } -
class Solution { public: vector<vector<int>> colorRed(int n) { vector<vector<int>> ans; ans.push_back({1, 1}); for (int i = n, k = 0; i > 1; --i, k = (k + 1) % 4) { if (k == 0) { for (int j = 1; j < i << 1; j += 2) { ans.push_back({i, j}); } } else if (k == 1) { ans.push_back({i, 2}); } else if (k == 2) { for (int j = 3; j < i << 1; j += 2) { ans.push_back({i, j}); } } else { ans.push_back({i, 1}); } } return ans; } }; -
class Solution: def colorRed(self, n: int) -> List[List[int]]: ans = [[1, 1]] k = 0 for i in range(n, 1, -1): if k == 0: for j in range(1, i << 1, 2): ans.append([i, j]) elif k == 1: ans.append([i, 2]) elif k == 2: for j in range(3, i << 1, 2): ans.append([i, j]) else: ans.append([i, 1]) k = (k + 1) % 4 return ans -
func colorRed(n int) (ans [][]int) { ans = append(ans, []int{1, 1}) for i, k := n, 0; i > 1; i, k = i-1, (k+1)%4 { if k == 0 { for j := 1; j < i<<1; j += 2 { ans = append(ans, []int{i, j}) } } else if k == 1 { ans = append(ans, []int{i, 2}) } else if k == 2 { for j := 3; j < i<<1; j += 2 { ans = append(ans, []int{i, j}) } } else { ans = append(ans, []int{i, 1}) } } return } -
function colorRed(n: number): number[][] { const ans: number[][] = [[1, 1]]; for (let i = n, k = 0; i > 1; --i, k = (k + 1) % 4) { if (k === 0) { for (let j = 1; j < i << 1; j += 2) { ans.push([i, j]); } } else if (k === 1) { ans.push([i, 2]); } else if (k === 2) { for (let j = 3; j < i << 1; j += 2) { ans.push([i, j]); } } else { ans.push([i, 1]); } } return ans; }