Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2500.html
2500. Delete Greatest Value in Each Row
- Difficulty: Easy.
- Related Topics: Array, Sorting, Matrix.
- Similar Questions: Equal Row and Column Pairs.
Problem
You are given an m x n matrix grid consisting of positive integers.
Perform the following operation until grid becomes empty:
-
Delete the element with the greatest value from each row. If multiple such elements exist, delete any of them.
-
Add the maximum of deleted elements to the answer.
Note that the number of columns decreases by one after each operation.
Return the answer after performing the operations described above.
Example 1:
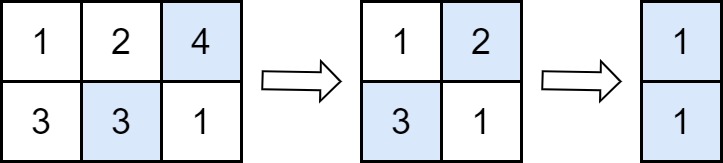
Input: grid = [[1,2,4],[3,3,1]]
Output: 8
Explanation: The diagram above shows the removed values in each step.
- In the first operation, we remove 4 from the first row and 3 from the second row (notice that, there are two cells with value 3 and we can remove any of them). We add 4 to the answer.
- In the second operation, we remove 2 from the first row and 3 from the second row. We add 3 to the answer.
- In the third operation, we remove 1 from the first row and 1 from the second row. We add 1 to the answer.
The final answer = 4 + 3 + 1 = 8.
Example 2:

Input: grid = [[10]]
Output: 10
Explanation: The diagram above shows the removed values in each step.
- In the first operation, we remove 10 from the first row. We add 10 to the answer.
The final answer = 10.
Constraints:
-
m == grid.length -
n == grid[i].length -
1 <= m, n <= 50 -
1 <= grid[i][j] <= 100
Solution (Java, C++, Python)
-
class Solution { public int deleteGreatestValue(int[][] grid) { for (var row : grid) { Arrays.sort(row); } int ans = 0; for (int j = 0; j < grid[0].length; ++j) { int t = 0; for (int i = 0; i < grid.length; ++i) { t = Math.max(t, grid[i][j]); } ans += t; } return ans; } } -
class Solution { public: int deleteGreatestValue(vector<vector<int>>& grid) { for (auto& row : grid) sort(row.begin(), row.end()); int ans = 0; for (int j = 0; j < grid[0].size(); ++j) { int t = 0; for (int i = 0; i < grid.size(); ++i) { t = max(t, grid[i][j]); } ans += t; } return ans; } }; -
class Solution: def deleteGreatestValue(self, grid: List[List[int]]) -> int: for row in grid: row.sort() return sum(max(col) for col in zip(*grid)) -
func deleteGreatestValue(grid [][]int) (ans int) { for _, row := range grid { sort.Ints(row) } for j := range grid[0] { t := 0 for i := range grid { if t < grid[i][j] { t = grid[i][j] } } ans += t } return } -
function deleteGreatestValue(grid: number[][]): number { for (const row of grid) { row.sort((a, b) => a - b); } let ans = 0; for (let j = 0; j < grid[0].length; ++j) { let t = 0; for (let i = 0; i < grid.length; ++i) { t = Math.max(t, grid[i][j]); } ans += t; } return ans; } -
impl Solution { pub fn delete_greatest_value(grid: Vec<Vec<i32>>) -> i32 { let mut grid = grid; for i in 0..grid.len() { grid[i].sort(); } let mut ans = 0; for j in 0..grid[0].len() { let mut mx = 0; for i in 0..grid.len() { if grid[i][j] > mx { mx = grid[i][j]; } } ans += mx; } ans } }
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).