Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2482.html
2482. Difference Between Ones and Zeros in Row and Column
- Difficulty: Medium.
- Related Topics: .
- Similar Questions: 01 Matrix, Special Positions in a Binary Matrix, Remove All Ones With Row and Column Flips.
Problem
You are given a 0-indexed m x n binary matrix grid.
A 0-indexed m x n difference matrix diff is created with the following procedure:
-
Let the number of ones in the
ithrow beonesRowi. -
Let the number of ones in the
jthcolumn beonesColj. -
Let the number of zeros in the
ithrow bezerosRowi. -
Let the number of zeros in the
jthcolumn bezerosColj. -
diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj
Return the difference matrix diff.
Example 1:
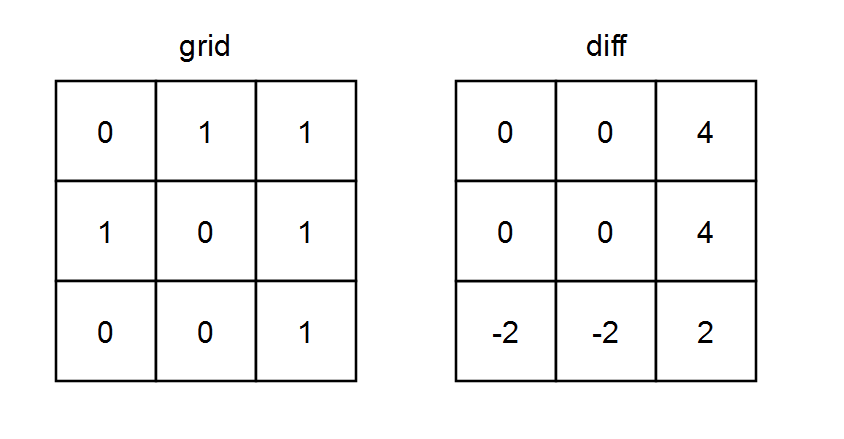
Input: grid = [[0,1,1],[1,0,1],[0,0,1]]
Output: [[0,0,4],[0,0,4],[-2,-2,2]]
Explanation:
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 2 + 1 - 1 - 2 = 0
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 2 + 1 - 1 - 2 = 0
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 2 + 3 - 1 - 0 = 4
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 2 + 1 - 1 - 2 = 0
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 2 + 1 - 1 - 2 = 0
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 2 + 3 - 1 - 0 = 4
- diff[2][0] = onesRow2 + onesCol0 - zerosRow2 - zerosCol0 = 1 + 1 - 2 - 2 = -2
- diff[2][1] = onesRow2 + onesCol1 - zerosRow2 - zerosCol1 = 1 + 1 - 2 - 2 = -2
- diff[2][2] = onesRow2 + onesCol2 - zerosRow2 - zerosCol2 = 1 + 3 - 2 - 0 = 2
Example 2:
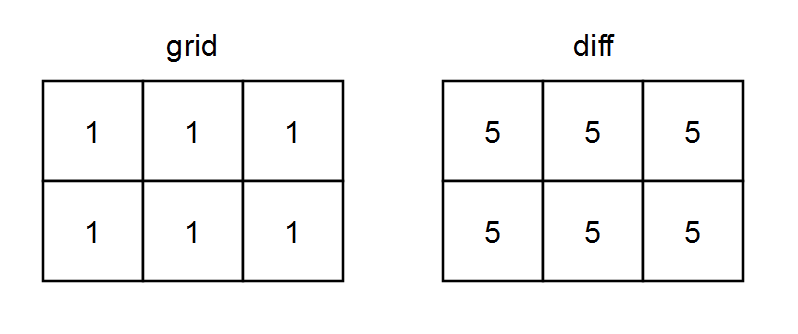
Input: grid = [[1,1,1],[1,1,1]]
Output: [[5,5,5],[5,5,5]]
Explanation:
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5
Constraints:
-
m == grid.length -
n == grid[i].length -
1 <= m, n <= 105 -
1 <= m * n <= 105 -
grid[i][j]is either0or1.
Solution (Java, C++, Python)
-
class Solution { public int[][] onesMinusZeros(int[][] grid) { int m = grid.length, n = grid[0].length; int[] rows = new int[m]; int[] cols = new int[n]; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { int v = grid[i][j]; rows[i] += v; cols[j] += v; } } int[][] diff = new int[m][n]; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { diff[i][j] = rows[i] + cols[j] - (n - rows[i]) - (m - cols[j]); } } return diff; } } -
class Solution { public: vector<vector<int>> onesMinusZeros(vector<vector<int>>& grid) { int m = grid.size(), n = grid[0].size(); vector<int> rows(m); vector<int> cols(n); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { int v = grid[i][j]; rows[i] += v; cols[j] += v; } } vector<vector<int>> diff(m, vector<int>(n)); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { diff[i][j] = rows[i] + cols[j] - (n - rows[i]) - (m - cols[j]); } } return diff; } }; -
class Solution: def onesMinusZeros(self, grid: List[List[int]]) -> List[List[int]]: m, n = len(grid), len(grid[0]) rows = [0] * m cols = [0] * n for i, row in enumerate(grid): for j, v in enumerate(row): rows[i] += v cols[j] += v diff = [[0] * n for _ in range(m)] for i, r in enumerate(rows): for j, c in enumerate(cols): diff[i][j] = r + c - (n - r) - (m - c) return diff -
func onesMinusZeros(grid [][]int) [][]int { m, n := len(grid), len(grid[0]) rows := make([]int, m) cols := make([]int, n) diff := make([][]int, m) for i, row := range grid { diff[i] = make([]int, n) for j, v := range row { rows[i] += v cols[j] += v } } for i, r := range rows { for j, c := range cols { diff[i][j] = r + c - (n - r) - (m - c) } } return diff } -
function onesMinusZeros(grid: number[][]): number[][] { const m = grid.length; const n = grid[0].length; const rows = new Array(m).fill(0); const cols = new Array(n).fill(0); for (let i = 0; i < m; i++) { for (let j = 0; j < n; j++) { if (grid[i][j]) { rows[i]++; cols[j]++; } } } const ans = Array.from({ length: m }, () => new Array(n).fill(0)); for (let i = 0; i < m; i++) { for (let j = 0; j < n; j++) { ans[i][j] = rows[i] + cols[j] - (m - rows[i]) - (n - cols[j]); } } return ans; } -
impl Solution { pub fn ones_minus_zeros(grid: Vec<Vec<i32>>) -> Vec<Vec<i32>> { let m = grid.len(); let n = grid[0].len(); let mut rows = vec![0; m]; let mut cols = vec![0; n]; for i in 0..m { for j in 0..n { if grid[i][j] == 1 { rows[i] += 1; cols[j] += 1; } } } let mut ans = vec![vec![0; n]; m]; for i in 0..m { for j in 0..n { ans[i][j] = (rows[i] + cols[j] - (m - rows[i]) - (n - cols[j])) as i32; } } ans } }
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(1).