Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2479.html
2479. Maximum XOR of Two Non-Overlapping Subtrees
Description
There is an undirected tree with n nodes labeled from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. The root of the tree is the node labeled 0.
Each node has an associated value. You are given an array values of length n, where values[i] is the value of the ith node.
Select any two non-overlapping subtrees. Your score is the bitwise XOR of the sum of the values within those subtrees.
Return the maximum possible score you can achieve. If it is impossible to find two nonoverlapping subtrees, return 0.
Note that:
- The subtree of a node is the tree consisting of that node and all of its descendants.
- Two subtrees are non-overlapping if they do not share any common node.
Example 1:
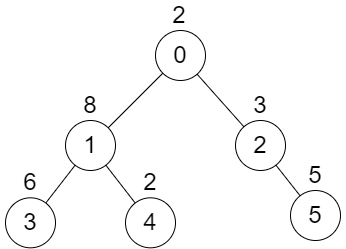
Input: n = 6, edges = [[0,1],[0,2],[1,3],[1,4],[2,5]], values = [2,8,3,6,2,5] Output: 24 Explanation: Node 1's subtree has sum of values 16, while node 2's subtree has sum of values 8, so choosing these nodes will yield a score of 16 XOR 8 = 24. It can be proved that is the maximum possible score we can obtain.
Example 2:
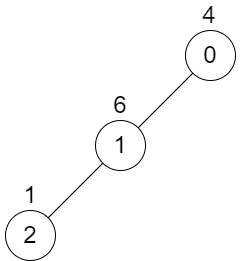
Input: n = 3, edges = [[0,1],[1,2]], values = [4,6,1] Output: 0 Explanation: There is no possible way to select two non-overlapping subtrees, so we just return 0.
Constraints:
2 <= n <= 5 * 104edges.length == n - 10 <= ai, bi < nvalues.length == n1 <= values[i] <= 109- It is guaranteed that
edgesrepresents a valid tree.
Solutions
-
class Trie { Trie[] children = new Trie[2]; void insert(long x) { Trie node = this; for (int i = 47; i >= 0; --i) { int v = (int) (x >> i) & 1; if (node.children[v] == null) { node.children[v] = new Trie(); } node = node.children[v]; } } long search(long x) { Trie node = this; long res = 0; for (int i = 47; i >= 0; --i) { int v = (int) (x >> i) & 1; if (node == null) { return res; } if (node.children[v ^ 1] != null) { res = res << 1 | 1; node = node.children[v ^ 1]; } else { res <<= 1; node = node.children[v]; } } return res; } } class Solution { private List<Integer>[] g; private int[] vals; private long[] s; private Trie tree; private long ans; public long maxXor(int n, int[][] edges, int[] values) { g = new List[n]; s = new long[n]; vals = values; Arrays.setAll(g, k -> new ArrayList<>()); for (var e : edges) { int a = e[0], b = e[1]; g[a].add(b); g[b].add(a); } dfs1(0, -1); tree = new Trie(); dfs2(0, -1); return ans; } private void dfs2(int i, int fa) { ans = Math.max(ans, tree.search(s[i])); for (int j : g[i]) { if (j != fa) { dfs2(j, i); } } tree.insert(s[i]); } private long dfs1(int i, int fa) { long t = vals[i]; for (int j : g[i]) { if (j != fa) { t += dfs1(j, i); } } s[i] = t; return t; } } -
using ll = long long; class Trie { public: vector<Trie*> children; string v; Trie() : children(2) {} void insert(ll x) { Trie* node = this; for (int i = 47; ~i; --i) { int v = (x >> i) & 1; if (!node->children[v]) node->children[v] = new Trie(); node = node->children[v]; } } ll search(ll x) { Trie* node = this; ll res = 0; for (int i = 47; ~i; --i) { if (!node) return res; int v = (x >> i) & 1; if (node->children[v ^ 1]) { res = res << 1 | 1; node = node->children[v ^ 1]; } else { res <<= 1; node = node->children[v]; } } return res; } }; class Solution { public: long long maxXor(int n, vector<vector<int>>& edges, vector<int>& values) { vector<vector<int>> g(n); for (auto& e : edges) { int a = e[0], b = e[1]; g[a].emplace_back(b); g[b].emplace_back(a); } vector<ll> s(n); function<ll(int, int)> dfs1 = [&](int i, int fa) -> ll { ll t = values[i]; for (int j : g[i]) { if (j != fa) t += dfs1(j, i); } s[i] = t; return t; }; dfs1(0, -1); Trie tree; ll ans = 0; function<void(int, int)> dfs2 = [&](int i, int fa) { ans = max(ans, tree.search(s[i])); for (int j : g[i]) { if (j != fa) { dfs2(j, i); } } tree.insert(s[i]); }; dfs2(0, -1); return ans; } }; -
class Trie: def __init__(self): self.children = [None] * 2 def insert(self, x): node = self for i in range(47, -1, -1): v = (x >> i) & 1 if node.children[v] is None: node.children[v] = Trie() node = node.children[v] def search(self, x): node = self res = 0 for i in range(47, -1, -1): v = (x >> i) & 1 if node is None: return res if node.children[v ^ 1]: res = res << 1 | 1 node = node.children[v ^ 1] else: res <<= 1 node = node.children[v] return res class Solution: def maxXor(self, n: int, edges: List[List[int]], values: List[int]) -> int: def dfs1(i, fa): t = values[i] for j in g[i]: if j != fa: t += dfs1(j, i) s[i] = t return t def dfs2(i, fa): nonlocal ans ans = max(ans, tree.search(s[i])) for j in g[i]: if j != fa: dfs2(j, i) tree.insert(s[i]) g = defaultdict(list) for a, b in edges: g[a].append(b) g[b].append(a) s = [0] * n dfs1(0, -1) ans = 0 tree = Trie() dfs2(0, -1) return ans -
type Trie struct { children [2]*Trie } func newTrie() *Trie { return &Trie{} } func (this *Trie) insert(x int) { node := this for i := 47; i >= 0; i-- { v := (x >> i) & 1 if node.children[v] == nil { node.children[v] = newTrie() } node = node.children[v] } } func (this *Trie) search(x int) int { node := this res := 0 for i := 47; i >= 0; i-- { v := (x >> i) & 1 if node == nil { return res } if node.children[v^1] != nil { res = res<<1 | 1 node = node.children[v^1] } else { res <<= 1 node = node.children[v] } } return res } func maxXor(n int, edges [][]int, values []int) int64 { g := make([][]int, n) for _, e := range edges { a, b := e[0], e[1] g[a] = append(g[a], b) g[b] = append(g[b], a) } s := make([]int, n) var dfs1 func(i, fa int) int dfs1 = func(i, fa int) int { t := values[i] for _, j := range g[i] { if j != fa { t += dfs1(j, i) } } s[i] = t return t } dfs1(0, -1) ans := 0 tree := newTrie() var dfs2 func(i, fa int) dfs2 = func(i, fa int) { ans = max(ans, tree.search(s[i])) for _, j := range g[i] { if j != fa { dfs2(j, i) } } tree.insert(s[i]) } dfs2(0, -1) return int64(ans) } func max(a, b int) int { if a > b { return a } return b }