2581. Count Number of Possible Root Nodes

Description

Alice has an undirected tree with n nodes labeled from 0 to n - 1. The tree is represented as a 2D integer array edges of length n - 1 where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the tree.

Alice wants Bob to find the root of the tree. She allows Bob to make several guesses about her tree. In one guess, he does the following:

Chooses two distinct integers u and v such that there exists an edge [u, v] in the tree.
He tells Alice that u is the parent of v in the tree.

Bob's guesses are represented by a 2D integer array guesses where guesses[j] = [u_j, v_j] indicates Bob guessed u_j to be the parent of v_j.

Alice being lazy, does not reply to each of Bob's guesses, but just says that at least k of his guesses are true.

Given the 2D integer arrays edges, guesses and the integer k, return the number of possible nodes that can be the root of Alice's tree. If there is no such tree, return 0.

Example 1:

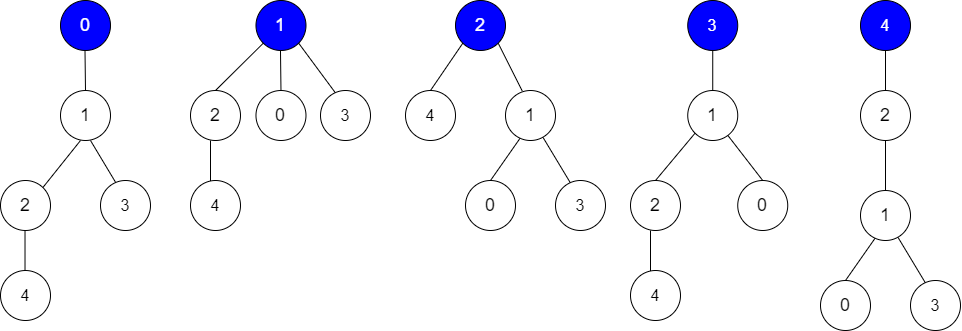
Input: edges = [[0,1],[1,2],[1,3],[4,2]], guesses = [[1,3],[0,1],[1,0],[2,4]], k = 3
Output: 3
Explanation: 
Root = 0, correct guesses = [1,3], [0,1], [2,4]
Root = 1, correct guesses = [1,3], [1,0], [2,4]
Root = 2, correct guesses = [1,3], [1,0], [2,4]
Root = 3, correct guesses = [1,0], [2,4]
Root = 4, correct guesses = [1,3], [1,0]
Considering 0, 1, or 2 as root node leads to 3 correct guesses.

Example 2:

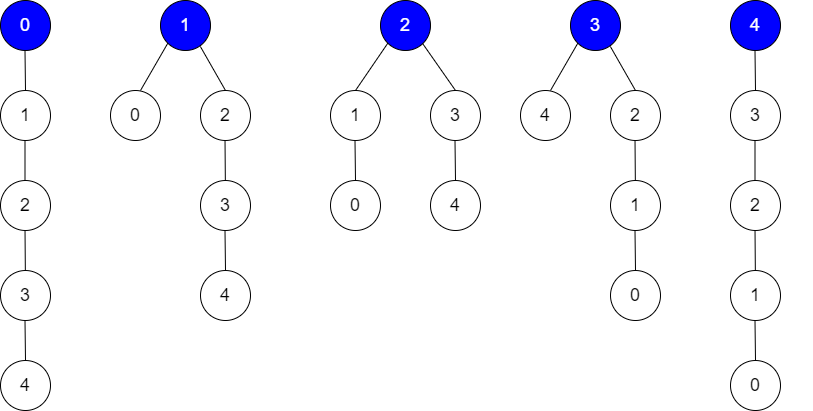
Input: edges = [[0,1],[1,2],[2,3],[3,4]], guesses = [[1,0],[3,4],[2,1],[3,2]], k = 1
Output: 5
Explanation: 
Root = 0, correct guesses = [3,4]
Root = 1, correct guesses = [1,0], [3,4]
Root = 2, correct guesses = [1,0], [2,1], [3,4]
Root = 3, correct guesses = [1,0], [2,1], [3,2], [3,4]
Root = 4, correct guesses = [1,0], [2,1], [3,2]
Considering any node as root will give at least 1 correct guess.

Constraints:

edges.length == n - 1
2 <= n <= 10⁵
1 <= guesses.length <= 10⁵
0 <= a_i, b_i, u_j, v_j <= n - 1
a_i != b_i
u_j != v_j
edges represents a valid tree.
guesses[j] is an edge of the tree.
guesses is unique.
0 <= k <= guesses.length

Solutions

Solution 1: Tree DP (change root)

First, we traverse the given edge set $edges$ and convert it to an adjacency list $g$ where $g[i]$ represents the adjacent nodes of node $i$. Use a hash map $gs$ to record the given guess set $guesses$.

Then, we start from node $0$ and perform a DFS to count the number of edges in $guesses$ among all the nodes that can be reached from node $0$. We use the variable $cnt$ to record this number.

Next, we start from node $0$ and perform a DFS to count the number of edges in $guesses$ in each tree with $0$ as the root. If the number is greater than or equal to $k$, it means that this node is a possible root node, and we add $1$ to the answer.

Therefore, the problem becomes to count the number of edges in $guesses$ in each tree with each node as the root. We already know that there are $cnt$ edges in $guesses$ among all the nodes that can be reached from node $0$. We can maintain this value by adding or subtracting the current edge in $guesses$ in DFS.

Assume that we are currently traversing node $i$ and $cnt$ represents the number of edges in $guesses$ with $i$ as the root node. Then, for each adjacent node $j$ of $i$, we need to calculate the number of edges in $guesses$ with $j$ as the root node. If $(i, j)$ is in $guesses$, then there is no edge $(i, j)$ in the tree with $j$ as the root node, so $cnt$ should decrease by $1$. If $(j, i)$ is in $guesses$, then there is an extra edge $(i, j)$ in the tree with $j$ as the root node, so $cnt$ should increase by $1$. That is, $f[j] = f[i] + (j, i) \in guesses - (i, j) \in guesses$. Where $f[i]$ represents the number of edges in $guesses$ with $i$ as the root node.

The time complexity is $O(n + m)$ and the space complexity is $O(n + m)$, where $n$ and $m$ are the lengths of $edges$ and $guesses$ respectively.

class Solution {
    private List<Integer>[] g;
    private Map<Long, Integer> gs = new HashMap<>();
    private int ans;
    private int k;
    private int cnt;
    private int n;

    public int rootCount(int[][] edges, int[][] guesses, int k) {
        this.k = k;
        n = edges.length + 1;
        g = new List[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        for (var e : guesses) {
            int a = e[0], b = e[1];
            gs.merge(f(a, b), 1, Integer::sum);
        }
        dfs1(0, -1);
        dfs2(0, -1);
        return ans;
    }

    private void dfs1(int i, int fa) {
        for (int j : g[i]) {
            if (j != fa) {
                cnt += gs.getOrDefault(f(i, j), 0);
                dfs1(j, i);
            }
        }
    }

    private void dfs2(int i, int fa) {
        ans += cnt >= k ? 1 : 0;
        for (int j : g[i]) {
            if (j != fa) {
                int a = gs.getOrDefault(f(i, j), 0);
                int b = gs.getOrDefault(f(j, i), 0);
                cnt -= a;
                cnt += b;
                dfs2(j, i);
                cnt -= b;
                cnt += a;
            }
        }
    }

    private long f(int i, int j) {
        return 1L * i * n + j;
    }
}

class Solution {
public:
    int rootCount(vector<vector<int>>& edges, vector<vector<int>>& guesses, int k) {
        int n = edges.size() + 1;
        vector<vector<int>> g(n);
        unordered_map<long long, int> gs;
        auto f = [&](int i, int j) {
            return 1LL * i * n + j;
        };
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        for (auto& e : guesses) {
            int a = e[0], b = e[1];
            gs[f(a, b)]++;
        }
        int ans = 0;
        int cnt = 0;

        function<void(int, int)> dfs1 = [&](int i, int fa) {
            for (int& j : g[i]) {
                if (j != fa) {
                    cnt += gs[f(i, j)];
                    dfs1(j, i);
                }
            }
        };

        function<void(int, int)> dfs2 = [&](int i, int fa) {
            ans += cnt >= k;
            for (int& j : g[i]) {
                if (j != fa) {
                    int a = gs[f(i, j)];
                    int b = gs[f(j, i)];
                    cnt -= a;
                    cnt += b;
                    dfs2(j, i);
                    cnt -= b;
                    cnt += a;
                }
            }
        };
        dfs1(0, -1);
        dfs2(0, -1);
        return ans;
    }
};

class Solution:
    def rootCount(
        self, edges: List[List[int]], guesses: List[List[int]], k: int
    ) -> int:
        def dfs1(i, fa):
            nonlocal cnt
            for j in g[i]:
                if j != fa:
                    cnt += gs[(i, j)]
                    dfs1(j, i)

        def dfs2(i, fa):
            nonlocal ans, cnt
            ans += cnt >= k
            for j in g[i]:
                if j != fa:
                    cnt -= gs[(i, j)]
                    cnt += gs[(j, i)]
                    dfs2(j, i)
                    cnt -= gs[(j, i)]
                    cnt += gs[(i, j)]

        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        gs = Counter((u, v) for u, v in guesses)
        cnt = 0
        dfs1(0, -1)
        ans = 0
        dfs2(0, -1)
        return ans

func rootCount(edges [][]int, guesses [][]int, k int) (ans int) {
	n := len(edges) + 1
	g := make([][]int, n)
	gs := map[int]int{}
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	f := func(i, j int) int {
		return i*n + j
	}
	for _, e := range guesses {
		a, b := e[0], e[1]
		gs[f(a, b)]++
	}

	cnt := 0
	var dfs1 func(i, fa int)
	var dfs2 func(i, fa int)
	dfs1 = func(i, fa int) {
		for _, j := range g[i] {
			if j != fa {
				cnt += gs[f(i, j)]
				dfs1(j, i)
			}
		}
	}
	dfs2 = func(i, fa int) {
		if cnt >= k {
			ans++
		}
		for _, j := range g[i] {
			if j != fa {
				a, b := gs[f(i, j)], gs[f(j, i)]
				cnt -= a
				cnt += b
				dfs2(j, i)
				cnt -= b
				cnt += a
			}
		}
	}
	dfs1(0, -1)
	dfs2(0, -1)
	return
}

function rootCount(edges: number[][], guesses: number[][], k: number): number {
    const n = edges.length + 1;
    const g: number[][] = Array.from({ length: n }, () => []);
    const gs: Map<number, number> = new Map();
    const f = (i: number, j: number) => i * n + j;
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    for (const [a, b] of guesses) {
        const x = f(a, b);
        gs.set(x, gs.has(x) ? gs.get(x)! + 1 : 1);
    }
    let ans = 0;
    let cnt = 0;
    const dfs1 = (i: number, fa: number): void => {
        for (const j of g[i]) {
            if (j !== fa) {
                cnt += gs.get(f(i, j)) || 0;
                dfs1(j, i);
            }
        }
    };
    const dfs2 = (i: number, fa: number): void => {
        ans += cnt >= k ? 1 : 0;
        for (const j of g[i]) {
            if (j !== fa) {
                const a = gs.get(f(i, j)) || 0;
                const b = gs.get(f(j, i)) || 0;
                cnt -= a;
                cnt += b;
                dfs2(j, i);
                cnt -= b;
                cnt += a;
            }
        }
    };
    dfs1(0, -1);
    dfs2(0, -1);
    return ans;
}

2581 - Count Number of Possible Root Nodes

2581. Count Number of Possible Root Nodes

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

2581. Count Number of Possible Root Nodes

Description

Solutions

All Problems

All Solutions