Welcome to Subscribe On Youtube
2579. Count Total Number of Colored Cells
Description
There exists an infinitely large two-dimensional grid of uncolored unit cells. You are given a positive integer n, indicating that you must do the following routine for n minutes:
- At the first minute, color any arbitrary unit cell blue.
- Every minute thereafter, color blue every uncolored cell that touches a blue cell.
Below is a pictorial representation of the state of the grid after minutes 1, 2, and 3.
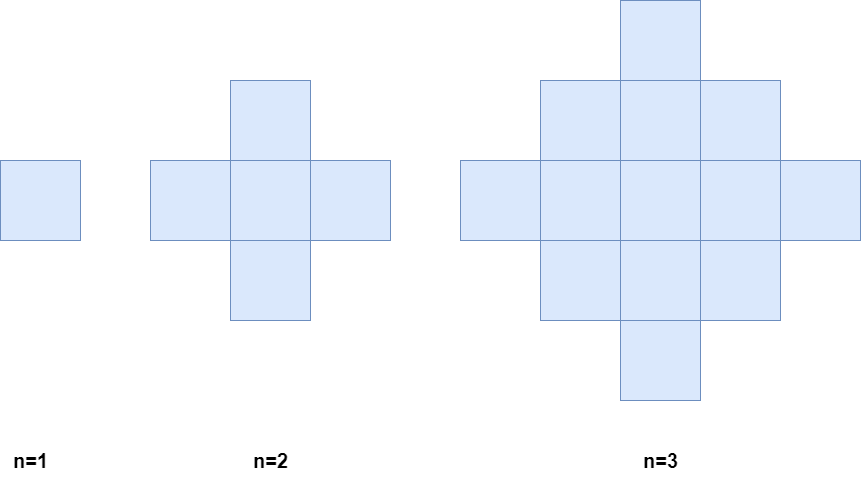
Return the number of colored cells at the end of n minutes.
Example 1:
Input: n = 1 Output: 1 Explanation: After 1 minute, there is only 1 blue cell, so we return 1.
Example 2:
Input: n = 2 Output: 5 Explanation: After 2 minutes, there are 4 colored cells on the boundary and 1 in the center, so we return 5.
Constraints:
1 <= n <= 105
Solutions
Solution 1: Mathematics
We find that after the $n$th minute, there are a total of $2 \times n - 1$ columns in the grid, and the numbers on each column are respectively $1, 3, 5, \cdots, 2 \times n - 1, 2 \times n - 3, \cdots, 3, 1$. The left and right parts are both arithmetic progressions, and the sum can be obtained by $2 \times n \times (n - 1) + 1$.
The time complexity is $O(1)$, and the space complexity is $O(1)$.
-
class Solution { public long coloredCells(int n) { return 2L * n * (n - 1) + 1; } } -
class Solution { public: long long coloredCells(int n) { return 2LL * n * (n - 1) + 1; } }; -
class Solution: def coloredCells(self, n: int) -> int: return 2 * n * (n - 1) + 1 -
func coloredCells(n int) int64 { return int64(2*n*(n-1) + 1) } -
function coloredCells(n: number): number { return 2 * n * (n - 1) + 1; } -
impl Solution { pub fn colored_cells(n: i32) -> i64 { 2 * (n as i64) * ((n as i64) - 1) + 1 } }