Welcome to Subscribe On Youtube

Formatted question description: https://leetcode.ca/all/2435.html

2435. Paths in Matrix Whose Sum Is Divisible by K

• Difficulty: Hard.
• Related Topics: Array, Dynamic Programming, Matrix.
• Similar Questions: Unique Paths, Unique Paths II, Minimum Path Sum, Dungeon Game, Cherry Pickup, Shortest Path in Binary Matrix, Minimum Cost Homecoming of a Robot in a Grid.

Problem

You are given a 0-indexed m x n integer matrix grid and an integer k. You are currently at position (0, 0) and you want to reach position (m - 1, n - 1) moving only down or right.

Return** the number of paths where the sum of the elements on the path is divisible by k. Since the answer may be very large, return it **modulo 10^9 + 7.

  Example 1:

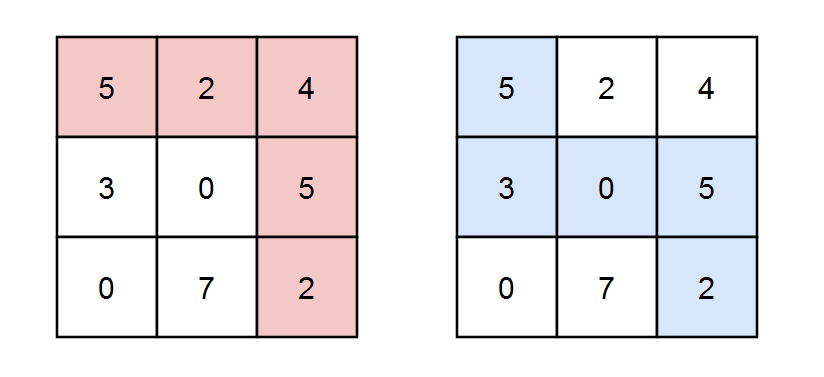
Input: grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3
Output: 2
Explanation: There are two paths where the sum of the elements on the path is divisible by k.
The first path highlighted in red has a sum of 5 + 2 + 4 + 5 + 2 = 18 which is divisible by 3.
The second path highlighted in blue has a sum of 5 + 3 + 0 + 5 + 2 = 15 which is divisible by 3.

Example 2:

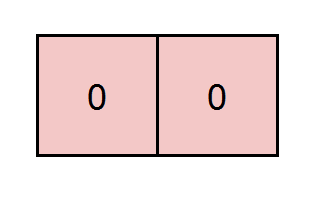
Input: grid = [[0,0]], k = 5
Output: 1
Explanation: The path highlighted in red has a sum of 0 + 0 = 0 which is divisible by 5.

Example 3:

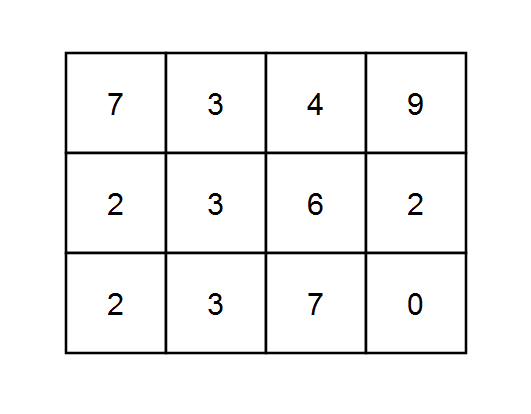
Input: grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1
Output: 10
Explanation: Every integer is divisible by 1 so the sum of the elements on every possible path is divisible by k.

  Constraints:

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 5 * 10^4

• 1 <= m * n <= 5 * 10^4

• 0 <= grid[i][j] <= 100

• 1 <= k <= 50

Solution (Java, C++, Python)

• Java
• C++
• Python
• Go
• TypeScript

• class Solution {
      private static final int MOD = (int) 1e9 + 7;
      
      public int numberOfPaths(int[][] grid, int k) {
          int m = grid.length, n = grid[0].length;
          int[][][] dp = new int[m][n][k];
          dp[0][0][grid[0][0] % k] = 1;
          for (int i = 0; i < m; ++i) {
              for (int j = 0; j < n; ++j) {
                  for (int s = 0; s < k; ++s) {
                      int t = ((s - grid[i][j] % k) + k) % k;
                      if (i > 0) {
                          dp[i][j][s] += dp[i - 1][j][t];
                      }
                      if (j > 0) {
                          dp[i][j][s] += dp[i][j - 1][t];
                      }
                      dp[i][j][s] %= MOD;
                  }
              }
          }
          return dp[m - 1][n - 1][0];
      }
  }
  
  

• class Solution {
  public:
      int numberOfPaths(vector<vector<int>>& grid, int k) {
          int m = grid.size(), n = grid[0].size();
          int mod = 1e9 + 7;
          vector<vector<vector<int>>> f(m, vector<vector<int>>(n, vector<int>(k, -1)));
          function<int(int, int, int)> dfs;
          dfs = [&](int i, int j, int s) {
              if (i < 0 || i >= m || j < 0 || j >= n) return 0;
              s = (s + grid[i][j]) % k;
              if (i == m - 1 && j == n - 1) return s == 0 ? 1 : 0;
              if (f[i][j][s] != -1) return f[i][j][s];
              int ans = dfs(i + 1, j, s) + dfs(i, j + 1, s);
              ans %= mod;
              f[i][j][s] = ans;
              return ans;
          };
          return dfs(0, 0, 0);
      }
  };
  

• class Solution:
      def numberOfPaths(self, grid: List[List[int]], k: int) -> int:
          m, n = len(grid), len(grid[0])
          dp = [[[0] * k for _ in range(n)] for _ in range(m)]
          dp[0][0][grid[0][0] % k] = 1
          mod = 10**9 + 7
          for i in range(m):
              for j in range(n):
                  for s in range(k):
                      t = ((s - grid[i][j] % k) + k) % k
                      if i:
                          dp[i][j][s] += dp[i - 1][j][t]
                      if j:
                          dp[i][j][s] += dp[i][j - 1][t]
                      dp[i][j][s] %= mod
          return dp[-1][-1][0]
  
  

• func numberOfPaths(grid [][]int, k int) int {
  	m, n := len(grid), len(grid[0])
  	var mod int = 1e9 + 7
  	f := make([][][]int, m)
  	for i := range f {
  		f[i] = make([][]int, n)
  		for j := range f[i] {
  			f[i][j] = make([]int, k)
  			for x := 0; x < k; x++ {
  				f[i][j][x] = -1
  			}
  		}
  	}
  	var dfs func(i, j, s int) int
  	dfs = func(i, j, s int) int {
  		if i < 0 || i >= m || j < 0 || j >= n {
  			return 0
  		}
  		s = (s + grid[i][j]) % k
  		if i == m-1 && j == n-1 {
  			if s == 0 {
  				return 1
  			}
  			return 0
  		}
  		if f[i][j][s] != -1 {
  			return f[i][j][s]
  		}
  		ans := dfs(i+1, j, s) + dfs(i, j+1, s)
  		ans %= mod
  		f[i][j][s] = ans
  		return ans
  	}
  	return dfs(0, 0, 0)
  }
  

• function numberOfPaths(grid: number[][], k: number): number {
      const MOD = 10 ** 9 + 7;
      const m = grid.length,
          n = grid[0].length;
      let ans = Array.from({ length: m + 1 }, () =>
          Array.from({ length: n + 1 }, () => new Array(k).fill(0)),
      );
      ans[0][1][0] = 1;
      for (let i = 0; i < m; i++) {
          for (let j = 0; j < n; j++) {
              for (let v = 0; v < k; v++) {
                  let key = (grid[i][j] + v) % k;
                  ans[i + 1][j + 1][key] =
                      (ans[i][j + 1][v] +
                          ans[i + 1][j][v] +
                          ans[i + 1][j + 1][key]) %
                      MOD;
              }
          }
      }
      return ans[m][n][0];
  }
  
  

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).

All Problems

All Solutions