Formatted question description: https://leetcode.ca/all/2397.html

2397. Maximum Rows Covered by Columns

Difficulty: Medium.
Related Topics: Array, Backtracking, Bit Manipulation, Matrix, Enumeration.
Similar Questions: Matchsticks to Square, Partition to K Equal Sum Subsets, Find the Shortest Superstring, Smallest Sufficient Team, Fair Distribution of Cookies.

Problem

You are given a 0-indexed m x n binary matrix matrix and an integer numSelect, which denotes the number of distinct columns you must select from matrix.

Let us consider s = {c1, c2, ...., cnumSelect} as the set of columns selected by you. A row row is covered by s if:

For each cell matrix[row][col] (0 <= col <= n - 1) where matrix[row][col] == 1, col is present in s or,
No cell in row has a value of 1.

You need to choose numSelect columns such that the number of rows that are covered is maximized.

Return the **maximum number of rows that can be covered by a set of numSelect columns.**

Example 1:

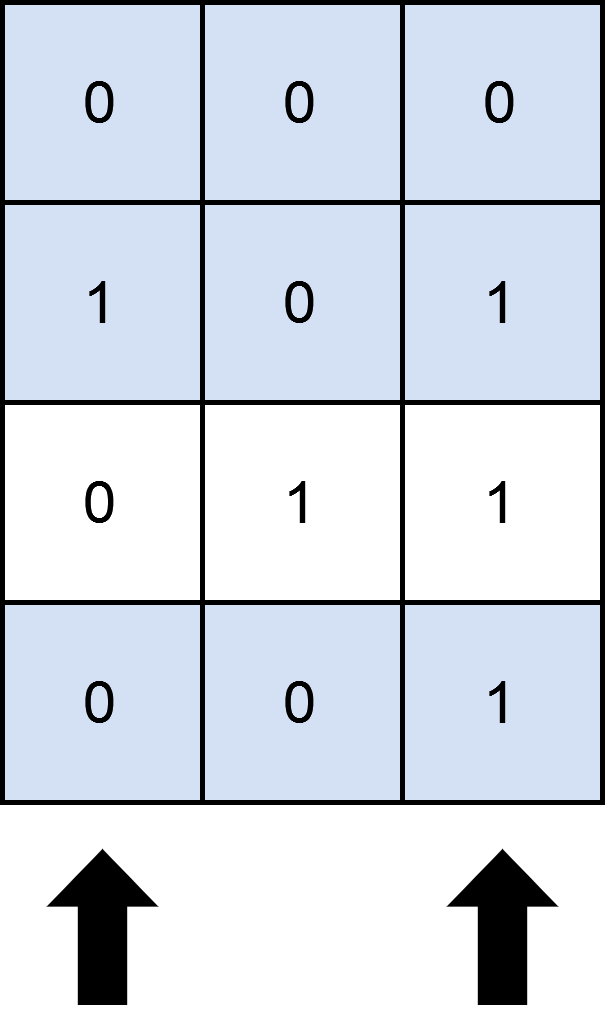
Input: matrix = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], numSelect = 2
Output: 3
Explanation: One possible way to cover 3 rows is shown in the diagram above.
We choose s = {0, 2}.
- Row 0 is covered because it has no occurrences of 1.
- Row 1 is covered because the columns with value 1, i.e. 0 and 2 are present in s.
- Row 2 is not covered because matrix[2][1] == 1 but 1 is not present in s.
- Row 3 is covered because matrix[2][2] == 1 and 2 is present in s.
Thus, we can cover three rows.
Note that s = {1, 2} will also cover 3 rows, but it can be shown that no more than three rows can be covered.

Example 2:

Input: matrix = [[1],[0]], numSelect = 1
Output: 2
Explanation: Selecting the only column will result in both rows being covered since the entire matrix is selected.
Therefore, we return 2.

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 12
matrix[i][j] is either 0 or 1.
1 <= numSelect <= n

Solution (Java, C++, Python)

class Solution {
    public int maximumRows(int[][] mat, int cols) {
        
        int m=mat.length;
        int n=mat[0].length;
        
        int[] s=new int[n];
        
        return f(0,m,n,cols,mat,s);
    }
    
    public int f(int ind,int m,int n,int cols,int[][] mat,int[] s){
        
        if(cols==0){
            int count=0;
            for(int i=0; i<m; i++){
			//supposing that this row is valid
                boolean selected=true;
                for(int j=0; j<n; j++){
				//if any cell of this row violates the given two conditions, then the row is discarded
                    if(mat[i][j]==1 && s[j]!=1)
                        selected=false;
                }
                if(selected)
                    count+=1;
            }
            
            return count;
        }
        
        int ans=-1;
        for(int i=ind; i<n; i++){
            
            s[i]=1; //do
            ans=Math.max(ans,f(i+1,m,n,cols-1,mat,s));
            s[i]=0; //undo / backtrack
        }
        
        return ans;
    }
}

############

class Solution {
    private int ans;
    public int maximumRows(int[][] mat, int cols) {
        int m = mat.length, n = mat[0].length;
        int[] arr = new int[m];
        for (int i = 0; i < m; ++i) {
            int x = 0;
            for (int j = 0; j < n; ++j) {
                x |= mat[i][j] << j;
            }
            arr[i] = x;
        }
        int ans = 0;
        for (int mask = 1; mask <= 1 << n; ++mask) {
            if (Integer.bitCount(mask) > cols) {
                continue;
            }
            int t = 0;
            for (int v : arr) {
                if ((v & mask) == v) {
                    ++t;
                }
            }
            ans = Math.max(ans, t);
        }
        return ans;
    }
}

class Solution:
    def maximumRows(self, mat: List[List[int]], cols: int) -> int:
        arr = []
        for i, row in enumerate(mat):
            x = 0
            for j, v in enumerate(row):
                x |= v << j
            arr.append(x)
        ans, n = 0, len(mat[0])
        for mask in range(1, 1 << n | 1):
            if mask.bit_count() > cols:
                continue
            t = sum((v & mask) == v for v in arr)
            ans = max(ans, t)
        return ans

############

# 2397. Maximum Rows Covered by Columns
# https://leetcode.com/problems/maximum-rows-covered-by-columns/

class Solution:
    def maximumRows(self, mat: List[List[int]], k: int) -> int:
        rows, cols = len(mat), len(mat[0])
        res = 0
        
        A = list(range(cols))

        for comb in combinations(A, k):
            filled = 0
            
            for row in mat:
                ones = row.count(1)
                curr = 0
                
                for index in comb:
                    if row[index] == 1:
                        curr += 1
                
                if curr == ones:
                    filled += 1
                
            res = max(res, filled)
            
        return res

class Solution {
public:
    int maximumRows(vector<vector<int>>& mat, int cols) {
        int m = mat.size(), n = mat[0].size();
        vector<int> arr(m);
        for (int i = 0; i < m; ++i) {
            int x = 0;
            for (int j = 0; j < n; ++j) x |= mat[i][j] << j;
            arr[i] = x;
        }
        int ans = 0;
        for (int mask = 1; mask <= 1 << n; ++mask) {
            if (__builtin_popcount(mask) > cols) continue;
            int t = 0;
            for (int v : arr) t += (v & mask) == v;
            ans = max(ans, t);
        }
        return ans;
    }
};

func maximumRows(mat [][]int, cols int) int {
	m, n := len(mat), len(mat[0])
	arr := make([]int, m)
	for i, row := range mat {
		x := 0
		for j, v := range row {
			x |= v << j
		}
		arr[i] = x
	}
	ans := 0
	for mask := 1; mask <= 1<<n; mask++ {
		if bits.OnesCount(uint(mask)) != cols {
			continue
		}
		t := 0
		for _, v := range arr {
			if (v & mask) == v {
				t++
			}
		}
		ans = max(ans, t)
	}
	return ans
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

function maximumRows(matrix: number[][], numSelect: number): number {
    const [m, n] = [matrix.length, matrix[0].length];
    const rows: number[] = Array(m).fill(0);
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (matrix[i][j]) {
                rows[i] |= 1 << j;
            }
        }
    }
    let ans = 0;
    for (let mask = 1; mask < 1 << n; ++mask) {
        if (bitCount(mask) !== numSelect) {
            continue;
        }
        let t = 0;
        for (const x of rows) {
            if ((x & mask) === x) {
                ++t;
            }
        }
        ans = Math.max(ans, t);
    }
    return ans;
}

function bitCount(i: number): number {
    i = i - ((i >>> 1) & 0x55555555);
    i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
    i = (i + (i >>> 4)) & 0x0f0f0f0f;
    i = i + (i >>> 8);
    i = i + (i >>> 16);
    return i & 0x3f;
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).

2397 - Maximum Rows Covered by Columns

2397. Maximum Rows Covered by Columns

Problem

Solution (Java, C++, Python)

All Problems

All Solutions

Welcome to Subscribe On Youtube

2397. Maximum Rows Covered by Columns

Problem

Solution (Java, C++, Python)

All Problems

All Solutions