Formatted question description: https://leetcode.ca/all/2385.html

2385. Amount of Time for Binary Tree to Be Infected

Difficulty: Medium.
Related Topics: Tree, Depth-First Search, Breadth-First Search, Binary Tree.
Similar Questions: Maximum Depth of Binary Tree, Shortest Path to Get Food, All Nodes Distance K in Binary Tree.

Problem

You are given the root of a binary tree with unique values, and an integer start. At minute 0, an infection starts from the node with value start.

Each minute, a node becomes infected if:

The node is currently uninfected.
The node is adjacent to an infected node.

Return the number of minutes needed for the entire tree to be infected.

Example 1:

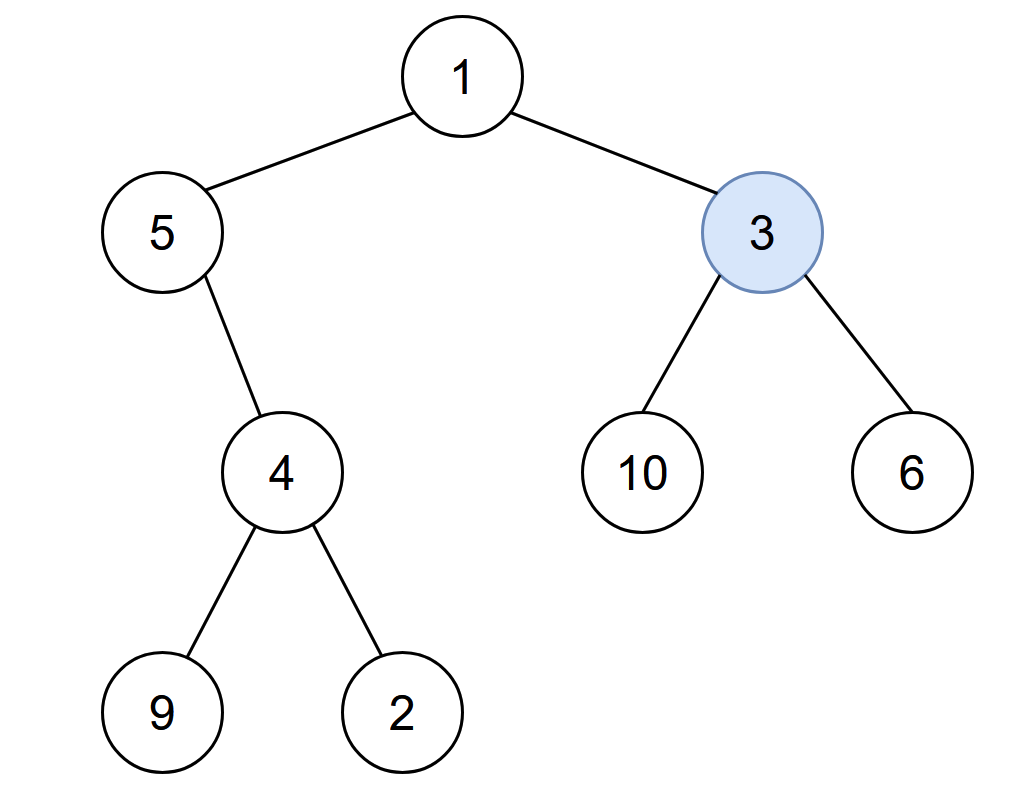
Input: root = [1,5,3,null,4,10,6,9,2], start = 3
Output: 4
Explanation: The following nodes are infected during:
- Minute 0: Node 3
- Minute 1: Nodes 1, 10 and 6
- Minute 2: Node 5
- Minute 3: Node 4
- Minute 4: Nodes 9 and 2
It takes 4 minutes for the whole tree to be infected so we return 4.

Example 2:

Input: root = [1], start = 1
Output: 0
Explanation: At minute 0, the only node in the tree is infected so we return 0.

Constraints:

The number of nodes in the tree is in the range [1, 105].
1 <= Node.val <= 105
Each node has a unique value.
A node with a value of start exists in the tree.

Solution (Java, C++, Python)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int max = 0;

    public int amountOfTime(TreeNode root, int start) {
        dfs(root, start, new Distance(-1));
        return max;
    }

    private int dfs(TreeNode root, int start, Distance l) {
        if (root == null) {
            return 0;
        }
        Distance ld = new Distance(-1);
        Distance rd = new Distance(-1);
        int left = dfs(root.left, start, ld);
        int right = dfs(root.right, start, rd);
        if (l.val == -1 && start == root.val) {
            max = Math.max(left, right);
            l.val = 1;
        }
        if (ld.val != -1) {
            max = Math.max(max, ld.val + right);
            l.val = ld.val + 1;
        } else if (rd.val != -1) {
            max = Math.max(max, rd.val + left);
            l.val = rd.val + 1;
        }
        return Math.max(left, right) + 1;
    }

    private static class Distance {
        int val;

        Distance(int v) {
            this.val = v;
        }
    }
}

############

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private Map<Integer, List<Integer>> g = new HashMap<>();

    public int amountOfTime(TreeNode root, int start) {
        dfs(root);
        Deque<Integer> q = new ArrayDeque<>();
        Set<Integer> vis = new HashSet<>();
        q.offer(start);
        int ans = -1;
        while (!q.isEmpty()) {
            ++ans;
            for (int n = q.size(); n > 0; --n) {
                int i = q.pollFirst();
                vis.add(i);
                if (g.containsKey(i)) {
                    for (int j : g.get(i)) {
                        if (!vis.contains(j)) {
                            q.offer(j);
                        }
                    }
                }
            }
        }
        return ans;
    }

    private void dfs(TreeNode root) {
        if (root == null) {
            return;
        }
        if (root.left != null) {
            g.computeIfAbsent(root.val, k -> new ArrayList<>()).add(root.left.val);
            g.computeIfAbsent(root.left.val, k -> new ArrayList<>()).add(root.val);
        }
        if (root.right != null) {
            g.computeIfAbsent(root.val, k -> new ArrayList<>()).add(root.right.val);
            g.computeIfAbsent(root.right.val, k -> new ArrayList<>()).add(root.val);
        }
        dfs(root.left);
        dfs(root.right);
    }
}

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:
        def dfs(root):
            if root is None:
                return
            if root.left:
                g[root.val].append(root.left.val)
                g[root.left.val].append(root.val)
            if root.right:
                g[root.val].append(root.right.val)
                g[root.right.val].append(root.val)
            dfs(root.left)
            dfs(root.right)

        g = defaultdict(list)
        dfs(root)
        vis = set()
        q = deque([start])
        ans = -1
        while q:
            ans += 1
            for _ in range(len(q)):
                i = q.popleft()
                vis.add(i)
                for j in g[i]:
                    if j not in vis:
                        q.append(j)
        return ans

############

# 2385. Amount of Time for Binary Tree to Be Infected
# https://leetcode.com/problems/amount-of-time-for-binary-tree-to-be-infected/

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:
        time = 0
        graph = defaultdict(list)
        N = 0
        
        def dfs(node):
            nonlocal N
            
            if not node: return
            
            N += 1    
            
            if node.left:
                graph[node.left.val].append(node.val)
                graph[node.val].append(node.left.val)
            
            if node.right:
                graph[node.right.val].append(node.val)
                graph[node.val].append(node.right.val)
            
            dfs(node.left)
            dfs(node.right)
        
        dfs(root)
        
        if N == 1: return 0
        
        s = [start]
        visited = defaultdict(lambda : False)
        visited[start] = True
        
        while s:
            nxt = []
            
            for node in s:
                for nei in graph[node]:
                    if not visited[nei]:
                        visited[nei] = True
                        nxt.append(nei)
            
            time += 1
            s = nxt
        
        return time - 1

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int, vector<int>> g;

    int amountOfTime(TreeNode* root, int start) {
        dfs(root);
        queue<int> q{ {start} };
        unordered_set<int> vis;
        int ans = -1;
        while (q.size()) {
            ++ans;
            for (int n = q.size(); n; --n) {
                int i = q.front();
                q.pop();
                vis.insert(i);
                for (int j : g[i]) {
                    if (!vis.count(j)) {
                        q.push(j);
                    }
                }
            }
        }
        return ans;
    }

    void dfs(TreeNode* root) {
        if (!root) return;
        if (root->left) {
            g[root->val].push_back(root->left->val);
            g[root->left->val].push_back(root->val);
        }
        if (root->right) {
            g[root->val].push_back(root->right->val);
            g[root->right->val].push_back(root->val);
        }
        dfs(root->left);
        dfs(root->right);
    }
};

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func amountOfTime(root *TreeNode, start int) int {
	g := map[int][]int{}
	var dfs func(*TreeNode)
	dfs = func(root *TreeNode) {
		if root == nil {
			return
		}
		if root.Left != nil {
			g[root.Val] = append(g[root.Val], root.Left.Val)
			g[root.Left.Val] = append(g[root.Left.Val], root.Val)
		}
		if root.Right != nil {
			g[root.Val] = append(g[root.Val], root.Right.Val)
			g[root.Right.Val] = append(g[root.Right.Val], root.Val)
		}
		dfs(root.Left)
		dfs(root.Right)
	}

	dfs(root)
	q := []int{start}
	ans := -1
	vis := map[int]bool{}
	for len(q) > 0 {
		ans++
		for n := len(q); n > 0; n-- {
			i := q[0]
			q = q[1:]
			vis[i] = true
			for _, j := range g[i] {
				if !vis[j] {
					q = append(q, j)
				}
			}
		}
	}
	return ans
}

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function amountOfTime(root: TreeNode | null, start: number): number {
    const map = new Map<number, number[]>();
    const create = ({ val, left, right }: TreeNode) => {
        if (left != null) {
            map.set(val, [...(map.get(val) ?? []), left.val]);
            map.set(left.val, [...(map.get(left.val) ?? []), val]);
            create(left);
        }
        if (right != null) {
            map.set(val, [...(map.get(val) ?? []), right.val]);
            map.set(right.val, [...(map.get(right.val) ?? []), val]);
            create(right);
        }
    };
    create(root);
    const dfs = (st: number, fa: number) => {
        let res = 0;
        for (const v of map.get(st) ?? []) {
            if (v !== fa) {
                res = Math.max(res, dfs(v, st) + 1);
            }
        }
        return res;
    };
    return dfs(start, -1);
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).

2385 - Amount of Time for Binary Tree to Be Infected

2385. Amount of Time for Binary Tree to Be Infected

Problem

Solution (Java, C++, Python)

All Problems

All Solutions

Welcome to Subscribe On Youtube

2385. Amount of Time for Binary Tree to Be Infected

Problem

Solution (Java, C++, Python)

All Problems

All Solutions