Formatted question description: https://leetcode.ca/all/2368.html

2368. Reachable Nodes With Restrictions

Difficulty: Medium.
Related Topics: Array, Hash Table, Tree, Depth-First Search, Breadth-First Search, Graph.
Similar Questions: Open the Lock, Minimum Jumps to Reach Home.

Problem

There is an undirected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. You are also given an integer array restricted which represents restricted nodes.

Return the **maximum number of nodes you can reach from node 0 without visiting a restricted node.**

Note that node 0 will not be a restricted node.

Example 1:

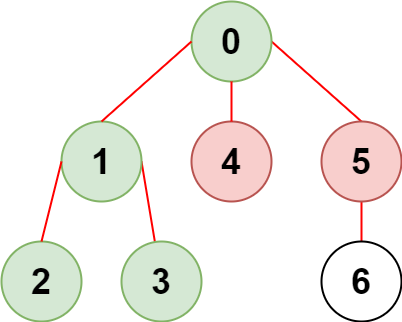
Input: n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
Output: 4
Explanation: The diagram above shows the tree.
We have that [0,1,2,3] are the only nodes that can be reached from node 0 without visiting a restricted node.

Example 2:

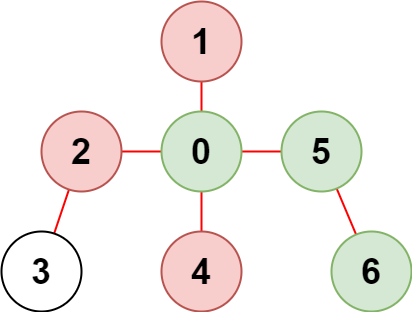
Input: n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
Output: 3
Explanation: The diagram above shows the tree.
We have that [0,5,6] are the only nodes that can be reached from node 0 without visiting a restricted node.

Constraints:

2 <= n <= 105
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
edges represents a valid tree.
1 <= restricted.length < n
1 <= restricted[i] < n
All the values of restricted are unique.

Solution (Java, C++, Python)

class Solution {
    public int reachableNodes(int n, int[][] edges, int[] restricted) {
        List<Integer>[] graph = new ArrayList[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int[] edge : edges) {
            int src = edge[0];
            int dest = edge[1];
            graph[src].add(dest);
            graph[dest].add(src);
        }
        Queue<Integer> q = new ArrayDeque<>();
        boolean[] visited = new boolean[n];
        q.offer(0);
        visited[0] = true;
        for (int node : restricted) {
            visited[node] = true;
        }
        int ans = 0;
        while (!q.isEmpty()) {
            int vertex = q.poll();
            ans++;
            for (int neighbour : graph[vertex]) {
                if (!visited[neighbour]) {
                    q.offer(neighbour);
                    visited[neighbour] = true;
                }
            }
        }
        return ans;
    }
}

############

class Solution {
    private List<Integer>[] g;
    private boolean[] vis;
    private int ans;

    public int reachableNodes(int n, int[][] edges, int[] restricted) {
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        vis = new boolean[n];
        for (int v : restricted) {
            vis[v] = true;
        }
        for (int[] e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }

        ans = 0;
        dfs(0);
        return ans;
    }

    private void dfs(int u) {
        if (vis[u]) {
            return;
        }
        ++ans;
        vis[u] = true;
        for (int v : g[u]) {
            dfs(v);
        }
    }
}

class Solution:
    def reachableNodes(
        self, n: int, edges: List[List[int]], restricted: List[int]
    ) -> int:
        g = defaultdict(list)
        vis = [False] * n
        for v in restricted:
            vis[v] = True
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)

        def dfs(u):
            nonlocal ans
            if vis[u]:
                return
            ans += 1
            vis[u] = True
            for v in g[u]:
                dfs(v)

        ans = 0
        dfs(0)
        return ans

############

# 2368. Reachable Nodes With Restrictions
# https://leetcode.com/problems/reachable-nodes-with-restrictions/

class Solution:
    def reachableNodes(self, n: int, edges: List[List[int]], restricted: List[int]) -> int:
        graph = defaultdict(list)
        visited = [False] * n
        blocked = set(restricted)
        
        for x, y in edges:
            graph[x].append(y)
            graph[y].append(x)
        
        res = 0
        
        def dfs(node):
            nonlocal res
            
            visited[node] = True
            
            res = 1
            
            for nei in graph[node]:
                if nei not in blocked and not visited[nei]:
                    res += dfs(nei)
            
            return res
            
        return dfs(0)
            
        

class Solution {
public:
    int ans;

    int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        vector<bool> vis(n);
        for (int v : restricted) vis[v] = true;
        ans = 0;
        dfs(0, g, vis);
        return ans;
    }

    void dfs(int u, vector<vector<int>>& g, vector<bool>& vis) {
        if (vis[u]) return;
        vis[u] = true;
        ++ans;
        for (int v : g[u]) dfs(v, g, vis);
    }
};

func reachableNodes(n int, edges [][]int, restricted []int) int {
	g := make([][]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	vis := make([]bool, n)
	for _, v := range restricted {
		vis[v] = true
	}
	ans := 0
	var dfs func(u int)
	dfs = func(u int) {
		if vis[u] {
			return
		}
		vis[u] = true
		ans++
		for _, v := range g[u] {
			dfs(v)
		}
	}
	dfs(0)
	return ans
}

function reachableNodes(
    n: number,
    edges: number[][],
    restricted: number[],
): number {
    let res = 0;
    const vis = new Array(n).fill(false);
    const map = new Map<number, number[]>();
    for (const [start, end] of edges) {
        map.set(start, [...(map.get(start) ?? []), end]);
        map.set(end, [...(map.get(end) ?? []), start]);
    }
    const dfs = (cur: number) => {
        if (restricted.includes(cur) || vis[cur]) {
            return;
        }
        res++;
        vis[cur] = true;
        for (const item of map.get(cur) ?? []) {
            dfs(item);
        }
    };
    dfs(0);

    return res;
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).

2368 - Reachable Nodes With Restrictions

2368. Reachable Nodes With Restrictions

Problem

Solution (Java, C++, Python)

All Problems

All Solutions

Welcome to Subscribe On Youtube

2368. Reachable Nodes With Restrictions

Problem

Solution (Java, C++, Python)

All Problems

All Solutions