Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2361.html
2361. Minimum Costs Using the Train Line
Description
A train line going through a city has two routes, the regular route and the express route. Both routes go through the same n + 1 stops labeled from 0 to n. Initially, you start on the regular route at stop 0.
You are given two 1-indexed integer arrays regular and express, both of length n. regular[i] describes the cost it takes to go from stop i - 1 to stop i using the regular route, and express[i] describes the cost it takes to go from stop i - 1 to stop i using the express route.
You are also given an integer expressCost which represents the cost to transfer from the regular route to the express route.
Note that:
- There is no cost to transfer from the express route back to the regular route.
- You pay
expressCostevery time you transfer from the regular route to the express route. - There is no extra cost to stay on the express route.
Return a 1-indexed array costs of length n, where costs[i] is the minimum cost to reach stop i from stop 0.
Note that a stop can be counted as reached from either route.
Example 1:
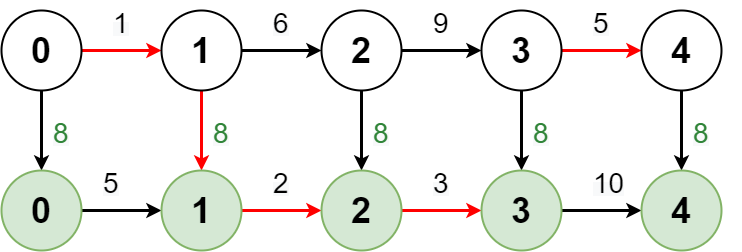
Input: regular = [1,6,9,5], express = [5,2,3,10], expressCost = 8 Output: [1,7,14,19] Explanation: The diagram above shows how to reach stop 4 from stop 0 with minimum cost. - Take the regular route from stop 0 to stop 1, costing 1. - Take the express route from stop 1 to stop 2, costing 8 + 2 = 10. - Take the express route from stop 2 to stop 3, costing 3. - Take the regular route from stop 3 to stop 4, costing 5. The total cost is 1 + 10 + 3 + 5 = 19. Note that a different route could be taken to reach the other stops with minimum cost.
Example 2:

Input: regular = [11,5,13], express = [7,10,6], expressCost = 3 Output: [10,15,24] Explanation: The diagram above shows how to reach stop 3 from stop 0 with minimum cost. - Take the express route from stop 0 to stop 1, costing 3 + 7 = 10. - Take the regular route from stop 1 to stop 2, costing 5. - Take the express route from stop 2 to stop 3, costing 3 + 6 = 9. The total cost is 10 + 5 + 9 = 24. Note that the expressCost is paid again to transfer back to the express route.
Constraints:
n == regular.length == express.length1 <= n <= 1051 <= regular[i], express[i], expressCost <= 105
Solutions
-
class Solution { public long[] minimumCosts(int[] regular, int[] express, int expressCost) { int n = regular.length; long f = 0; long g = 1 << 30; long[] cost = new long[n]; for (int i = 0; i < n; ++i) { int a = regular[i]; int b = express[i]; long ff = Math.min(f + a, g + a); long gg = Math.min(f + expressCost + b, g + b); f = ff; g = gg; cost[i] = Math.min(f, g); } return cost; } } -
class Solution { public: vector<long long> minimumCosts(vector<int>& regular, vector<int>& express, int expressCost) { int n = regular.size(); long long f = 0; long long g = 1 << 30; vector<long long> cost(n); for (int i = 0; i < n; ++i) { int a = regular[i]; int b = express[i]; long long ff = min(f + a, g + a); long long gg = min(f + expressCost + b, g + b); f = ff; g = gg; cost[i] = min(f, g); } return cost; } }; -
class Solution: def minimumCosts( self, regular: List[int], express: List[int], expressCost: int ) -> List[int]: n = len(regular) f, g = 0, inf cost = [0] * n for i, (a, b) in enumerate(zip(regular, express), 1): ff = min(f + a, g + a) gg = min(f + expressCost + b, g + b) f, g = ff, gg cost[i - 1] = min(f, g) return cost -
func minimumCosts(regular []int, express []int, expressCost int) []int64 { f, g := 0, 1<<30 cost := make([]int64, len(regular)) for i, a := range regular { b := express[i] ff := min(f+a, g+a) gg := min(f+expressCost+b, g+b) f, g = ff, gg cost[i] = int64(min(f, g)) } return cost } func min(a, b int) int { if a < b { return a } return b } -
function minimumCosts( regular: number[], express: number[], expressCost: number, ): number[] { const n = regular.length; let f = 0; let g = 1 << 30; const cost: number[] = new Array(n).fill(0); for (let i = 0; i < n; ++i) { const [a, b] = [regular[i], express[i]]; const ff = Math.min(f + a, g + a); const gg = Math.min(f + expressCost + b, g + b); [f, g] = [ff, gg]; cost[i] = Math.min(f, g); } return cost; }