Formatted question description: https://leetcode.ca/all/2359.html

2359. Find Closest Node to Given Two Nodes

Difficulty: Medium.
Related Topics: Depth-First Search, Graph.
Similar Questions: .

Problem

You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.

The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from i, then edges[i] == -1.

You are also given two integers node1 and node2.

Return the **index of the node that can be reached from both node1 and node2, such that the maximum between the distance from node1 to that node, and from node2 to that node is minimized. If there are multiple answers, return the node with the **smallest index, and if no possible answer exists, return -1.

Note that edges may contain cycles.

Example 1:

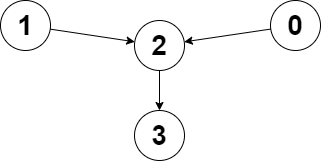
Input: edges = [2,2,3,-1], node1 = 0, node2 = 1
Output: 2
Explanation: The distance from node 0 to node 2 is 1, and the distance from node 1 to node 2 is 1.
The maximum of those two distances is 1. It can be proven that we cannot get a node with a smaller maximum distance than 1, so we return node 2.

Example 2:

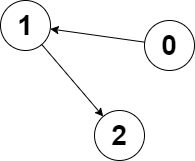
Input: edges = [1,2,-1], node1 = 0, node2 = 2
Output: 2
Explanation: The distance from node 0 to node 2 is 2, and the distance from node 2 to itself is 0.
The maximum of those two distances is 2. It can be proven that we cannot get a node with a smaller maximum distance than 2, so we return node 2.

Constraints:

n == edges.length
2 <= n <= 105
-1 <= edges[i] < n
edges[i] != i
0 <= node1, node2 < n

Solution (Java, C++, Python)

class Solution {
    public int closestMeetingNode(int[] edges, int node1, int node2) {
        final int n = edges.length;
        final Integer[] m1 = new Integer[n];
        final Integer[] m2 = new Integer[n];
        dfs(edges, m1, node1);
        dfs(edges, m2, node2);
        int index = -1;
        int dist = Integer.MAX_VALUE;
        for (int i = 0; i < n; i++) {
            if (m1[i] != null && m2[i] != null && dist > Math.max(m1[i], m2[i])) {
                dist = Math.max(m1[i], m2[i]);
                index = i;
            }
        }
        return index;
    }

    private void dfs(int[] edges, Integer[] memo, int node) {
        int dist = 0;
        while (node != -1 && memo[node] == null) {
            memo[node] = dist++;
            node = edges[node];
        }
    }
}

############

class Solution {
    private int n;
    private List<Integer>[] g;

    public int closestMeetingNode(int[] edges, int node1, int node2) {
        n = edges.length;
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (int i = 0; i < n; ++i) {
            if (edges[i] != -1) {
                g[i].add(edges[i]);
            }
        }
        int[] d1 = dijkstra(node1);
        int[] d2 = dijkstra(node2);
        int d = 1 << 30;
        int ans = -1;
        for (int i = 0; i < n; ++i) {
            int t = Math.max(d1[i], d2[i]);
            if (t < d) {
                d = t;
                ans = i;
            }
        }
        return ans;
    }

    private int[] dijkstra(int i) {
        int[] dist = new int[n];
        Arrays.fill(dist, 1 << 30);
        dist[i] = 0;
        PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[0] - b[0]);
        q.offer(new int[] {0, i});
        while (!q.isEmpty()) {
            var p = q.poll();
            i = p[1];
            for (int j : g[i]) {
                if (dist[j] > dist[i] + 1) {
                    dist[j] = dist[i] + 1;
                    q.offer(new int[] {dist[j], j});
                }
            }
        }
        return dist;
    }
}

class Solution {
 public:
  int closestMeetingNode(vector<int>& edges, int node1, int node2) {
    constexpr int kMax = 10000;
    const vector<int> dist1 = getDist(edges, node1);
    const vector<int> dist2 = getDist(edges, node2);
    int minDist = kMax;
    int ans = -1;

    for (int i = 0; i < edges.size(); ++i)
      if (min(dist1[i], dist2[i]) >= 0) {
        const int maxDist = max(dist1[i], dist2[i]);
        if (maxDist < minDist) {
          minDist = maxDist;
          ans = i;
        }
      }

    return ans;
  }

 private:
  vector<int> getDist(const vector<int>& edges, int u) {
    vector<int> dist(edges.size(), -1);
    int d = 0;
    while (u != -1 && dist[u] == -1) {
      dist[u] = d++;
      u = edges[u];
    }
    return dist;
  }
};

class Solution:
    def closestMeetingNode(self, edges: List[int], node1: int, node2: int) -> int:
        def dijkstra(g, u):
            dist = [inf] * n
            dist[u] = 0
            q = [(0, u)]
            while q:
                d, u = heappop(q)
                if d > dist[u]:
                    continue
                for v in g[u]:
                    if dist[v] > dist[u] + 1:
                        dist[v] = dist[u] + 1
                        heappush(q, (dist[v], v))
            return dist

        g = defaultdict(list)
        n = len(edges)
        for i, v in enumerate(edges):
            if v != -1:
                g[i].append(v)
        d1 = dijkstra(g, node1)
        d2 = dijkstra(g, node2)
        d = inf
        ans = -1
        for i, (a, b) in enumerate(zip(d1, d2)):
            if d > max(a, b):
                d = max(a, b)
                ans = i
        return ans

############

# 2359. Find Closest Node to Given Two Nodes
# https://leetcode.com/problems/find-closest-node-to-given-two-nodes/

class Solution:
    def closestMeetingNode(self, edges: List[int], node1: int, node2: int) -> int:
        n = len(edges)
        
        def gen(src):
            dist = [inf] * n
            dist[src] = 0
            
            pq = [(0, src)]
            
            while pq:
                weight, node = heappop(pq)
                
                if edges[node] == -1 or weight != dist[node]: continue
                    
                nei = edges[node]
                
                old = dist[nei]
                new = weight + 1
                
                if new < old:
                    dist[nei] = new
                    heappush(pq, (new, nei))
            
            return dist

        dist1 = gen(node1)
        dist2 = gen(node2)
        
        res = inf
        index = 0

        for i, (a, b) in enumerate(zip(dist1, dist2)):
            s = max(a, b)
            if s < res:
                res = s
                index = i
        
        return -1 if res == inf else index
        

func closestMeetingNode(edges []int, node1 int, node2 int) int {
	n := len(edges)
	g := make([][]int, n)
	for i, j := range edges {
		if j != -1 {
			g[i] = append(g[i], j)
		}
	}
	const inf int = 1 << 30
	dijkstra := func(i int) []int {
		dist := make([]int, n)
		for j := range dist {
			dist[j] = inf
		}
		dist[i] = 0
		q := hp{}
		heap.Push(&q, pair{0, i})
		for len(q) > 0 {
			i := heap.Pop(&q).(pair).i
			for _, j := range g[i] {
				if dist[j] > dist[i]+1 {
					dist[j] = dist[i] + 1
					heap.Push(&q, pair{dist[j], j})
				}
			}
		}
		return dist
	}
	d1 := dijkstra(node1)
	d2 := dijkstra(node2)
	ans, d := -1, inf
	for i, a := range d1 {
		b := d2[i]
		t := max(a, b)
		if t < d {
			d = t
			ans = i
		}
	}
	return ans
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

type pair struct{ d, i int }
type hp []pair

func (h hp) Len() int            { return len(h) }
func (h hp) Less(i, j int) bool  { return h[i].d < h[j].d }
func (h hp) Swap(i, j int)       { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v interface{}) { *h = append(*h, v.(pair)) }
func (h *hp) Pop() interface{}   { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }

function closestMeetingNode(
    edges: number[],
    node1: number,
    node2: number,
): number {
    const n = edges.length;
    const g = Array.from({ length: n }, () => []);
    for (let i = 0; i < n; ++i) {
        if (edges[i] != -1) {
            g[i].push(edges[i]);
        }
    }
    const inf = 1 << 30;
    const f = (i: number) => {
        const dist = new Array(n).fill(inf);
        dist[i] = 0;
        const q: number[] = [i];
        while (q.length) {
            i = q.shift();
            for (const j of g[i]) {
                if (dist[j] == inf) {
                    dist[j] = dist[i] + 1;
                    q.push(j);
                }
            }
        }
        return dist;
    };
    const d1 = f(node1);
    const d2 = f(node2);
    let ans = -1;
    let d = inf;
    for (let i = 0; i < n; ++i) {
        const t = Math.max(d1[i], d2[i]);
        if (t < d) {
            d = t;
            ans = i;
        }
    }
    return ans;
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).

2359 - Find Closest Node to Given Two Nodes

2359. Find Closest Node to Given Two Nodes

Problem

Solution (Java, C++, Python)

All Problems

All Solutions

Welcome to Subscribe On Youtube

2359. Find Closest Node to Given Two Nodes

Problem

Solution (Java, C++, Python)

All Problems

All Solutions