Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2345.html
2345. Finding the Number of Visible Mountains
Description
You are given a 0-indexed 2D integer array peaks where peaks[i] = [xi, yi] states that mountain i has a peak at coordinates (xi, yi). A mountain can be described as a right-angled isosceles triangle, with its base along the x-axis and a right angle at its peak. More formally, the gradients of ascending and descending the mountain are 1 and -1 respectively.
A mountain is considered visible if its peak does not lie within another mountain (including the border of other mountains).
Return the number of visible mountains.
Example 1:
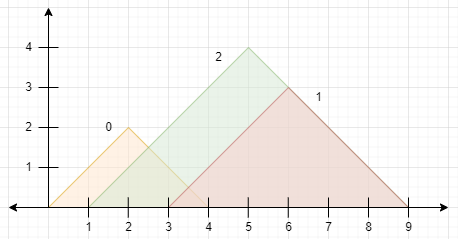
Input: peaks = [[2,2],[6,3],[5,4]] Output: 2 Explanation: The diagram above shows the mountains. - Mountain 0 is visible since its peak does not lie within another mountain or its sides. - Mountain 1 is not visible since its peak lies within the side of mountain 2. - Mountain 2 is visible since its peak does not lie within another mountain or its sides. There are 2 mountains that are visible.
Example 2:
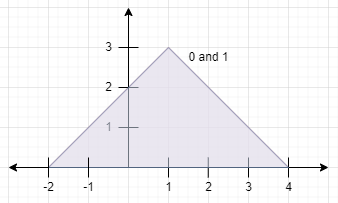
Input: peaks = [[1,3],[1,3]] Output: 0 Explanation: The diagram above shows the mountains (they completely overlap). Both mountains are not visible since their peaks lie within each other.
Constraints:
1 <= peaks.length <= 105peaks[i].length == 21 <= xi, yi <= 105
Solutions
-
class Solution { public int visibleMountains(int[][] peaks) { int n = peaks.length; int[][] arr = new int[n][2]; Map<String, Integer> cnt = new HashMap<>(); for (int i = 0; i < n; ++i) { int x = peaks[i][0], y = peaks[i][1]; arr[i] = new int[] {x - y, x + y}; cnt.merge((x - y) + "" + (x + y), 1, Integer::sum); } Arrays.sort(arr, (a, b) -> a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]); int ans = 0; int cur = Integer.MIN_VALUE; for (int[] e : arr) { int l = e[0], r = e[1]; if (r <= cur) { continue; } cur = r; if (cnt.get(l + "" + r) == 1) { ++ans; } } return ans; } } -
class Solution { public: int visibleMountains(vector<vector<int>>& peaks) { vector<pair<int, int>> arr; for (auto& e : peaks) { int x = e[0], y = e[1]; arr.emplace_back(x - y, -(x + y)); } sort(arr.begin(), arr.end()); int n = arr.size(); int ans = 0, cur = INT_MIN; for (int i = 0; i < n; ++i) { int l = arr[i].first, r = -arr[i].second; if (r <= cur) { continue; } cur = r; ans += i == n - 1 || (i < n - 1 && arr[i] != arr[i + 1]); } return ans; } }; -
class Solution: def visibleMountains(self, peaks: List[List[int]]) -> int: arr = [(x - y, x + y) for x, y in peaks] cnt = Counter(arr) arr.sort(key=lambda x: (x[0], -x[1])) ans, cur = 0, -inf for l, r in arr: if r <= cur: continue cur = r if cnt[(l, r)] == 1: ans += 1 return ans -
func visibleMountains(peaks [][]int) (ans int) { n := len(peaks) type pair struct{ l, r int } arr := make([]pair, n) for _, p := range peaks { x, y := p[0], p[1] arr = append(arr, pair{x - y, x + y}) } sort.Slice(arr, func(i, j int) bool { return arr[i].l < arr[j].l || (arr[i].l == arr[j].l && arr[i].r > arr[j].r) }) cur := math.MinInt32 for i, e := range arr { l, r := e.l, e.r if r <= cur { continue } cur = r if !(i < n-1 && l == arr[i+1].l && r == arr[i+1].r) { ans++ } } return }