Welcome to Subscribe On Youtube
2458. Height of Binary Tree After Subtree Removal Queries
Description
You are given the root of a binary tree with n nodes. Each node is assigned a unique value from 1 to n. You are also given an array queries of size m.
You have to perform m independent queries on the tree where in the ith query you do the following:
- Remove the subtree rooted at the node with the value
queries[i]from the tree. It is guaranteed thatqueries[i]will not be equal to the value of the root.
Return an array answer of size m where answer[i] is the height of the tree after performing the ith query.
Note:
- The queries are independent, so the tree returns to its initial state after each query.
- The height of a tree is the number of edges in the longest simple path from the root to some node in the tree.
Example 1:
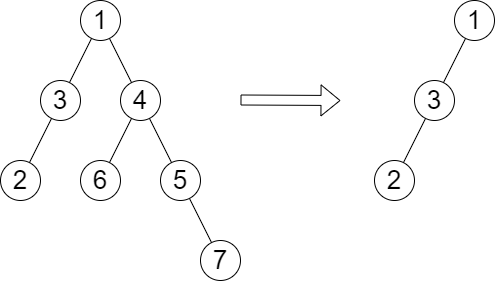
Input: root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4] Output: [2] Explanation: The diagram above shows the tree after removing the subtree rooted at node with value 4. The height of the tree is 2 (The path 1 -> 3 -> 2).
Example 2:
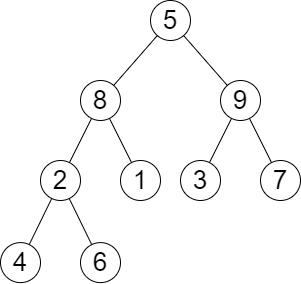
Input: root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8] Output: [3,2,3,2] Explanation: We have the following queries: - Removing the subtree rooted at node with value 3. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 4). - Removing the subtree rooted at node with value 2. The height of the tree becomes 2 (The path 5 -> 8 -> 1). - Removing the subtree rooted at node with value 4. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 6). - Removing the subtree rooted at node with value 8. The height of the tree becomes 2 (The path 5 -> 9 -> 3).
Constraints:
- The number of nodes in the tree is
n. 2 <= n <= 1051 <= Node.val <= n- All the values in the tree are unique.
m == queries.length1 <= m <= min(n, 104)1 <= queries[i] <= nqueries[i] != root.val
Solutions
Solution 1: Two DFS Traversals
First, we perform a DFS traversal to determine the depth of each node, which we store in a hash table $d$, where $d[x]$ represents the depth of node $x$.
Then we design a function $dfs(root, depth, rest)$, where:
rootrepresents the current node;depthrepresents the depth of the current node;restrepresents the height of the tree after deleting the current node.
The function’s computation logic is as follows:
If the node is null, return directly. Otherwise, we increment depth by $1$, and then store rest in res.
Next, we recursively traverse the left and right subtrees.
Before recursing into the left subtree, we calculate the depth from the root node to the deepest node in the current node’s right subtree, i.e., $depth+d[root.right]$, and then compare it with rest, taking the larger value as the rest for the left subtree.
Before recursing into the right subtree, we calculate the depth from the root node to the deepest node in the current node’s left subtree, i.e., $depth+d[root.left]$, and then compare it with rest, taking the larger value as the rest for the right subtree.
Finally, we return the result values corresponding to each query node.
The time complexity is $O(n+m)$, and the space complexity is $O(n)$. Here, $n$ and $m$ are the number of nodes in the tree and the number of queries, respectively.
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { private Map<TreeNode, Integer> d = new HashMap<>(); private int[] res; public int[] treeQueries(TreeNode root, int[] queries) { f(root); res = new int[d.size() + 1]; d.put(null, 0); dfs(root, -1, 0); int m = queries.length; int[] ans = new int[m]; for (int i = 0; i < m; ++i) { ans[i] = res[queries[i]]; } return ans; } private void dfs(TreeNode root, int depth, int rest) { if (root == null) { return; } ++depth; res[root.val] = rest; dfs(root.left, depth, Math.max(rest, depth + d.get(root.right))); dfs(root.right, depth, Math.max(rest, depth + d.get(root.left))); } private int f(TreeNode root) { if (root == null) { return 0; } int l = f(root.left), r = f(root.right); d.put(root, 1 + Math.max(l, r)); return d.get(root); } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: vector<int> treeQueries(TreeNode* root, vector<int>& queries) { unordered_map<TreeNode*, int> d; function<int(TreeNode*)> f = [&](TreeNode* root) -> int { if (!root) return 0; int l = f(root->left), r = f(root->right); d[root] = 1 + max(l, r); return d[root]; }; f(root); vector<int> res(d.size() + 1); function<void(TreeNode*, int, int)> dfs = [&](TreeNode* root, int depth, int rest) { if (!root) return; ++depth; res[root->val] = rest; dfs(root->left, depth, max(rest, depth + d[root->right])); dfs(root->right, depth, max(rest, depth + d[root->left])); }; dfs(root, -1, 0); vector<int> ans; for (int v : queries) ans.emplace_back(res[v]); return ans; } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def treeQueries(self, root: Optional[TreeNode], queries: List[int]) -> List[int]: def f(root): if root is None: return 0 l, r = f(root.left), f(root.right) d[root] = 1 + max(l, r) return d[root] def dfs(root, depth, rest): if root is None: return depth += 1 res[root.val] = rest dfs(root.left, depth, max(rest, depth + d[root.right])) dfs(root.right, depth, max(rest, depth + d[root.left])) d = defaultdict(int) f(root) res = [0] * (len(d) + 1) dfs(root, -1, 0) return [res[v] for v in queries] -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func treeQueries(root *TreeNode, queries []int) (ans []int) { d := map[*TreeNode]int{} var f func(*TreeNode) int f = func(root *TreeNode) int { if root == nil { return 0 } l, r := f(root.Left), f(root.Right) d[root] = 1 + max(l, r) return d[root] } f(root) res := make([]int, len(d)+1) var dfs func(*TreeNode, int, int) dfs = func(root *TreeNode, depth, rest int) { if root == nil { return } depth++ res[root.Val] = rest dfs(root.Left, depth, max(rest, depth+d[root.Right])) dfs(root.Right, depth, max(rest, depth+d[root.Left])) } dfs(root, -1, 0) for _, v := range queries { ans = append(ans, res[v]) } return }