Welcome to Subscribe On Youtube
2428. Maximum Sum of an Hourglass
Description
You are given an m x n integer matrix grid.
We define an hourglass as a part of the matrix with the following form:

Return the maximum sum of the elements of an hourglass.
Note that an hourglass cannot be rotated and must be entirely contained within the matrix.
Example 1:
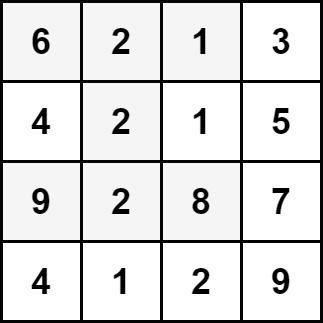
Input: grid = [[6,2,1,3],[4,2,1,5],[9,2,8,7],[4,1,2,9]] Output: 30 Explanation: The cells shown above represent the hourglass with the maximum sum: 6 + 2 + 1 + 2 + 9 + 2 + 8 = 30.
Example 2:
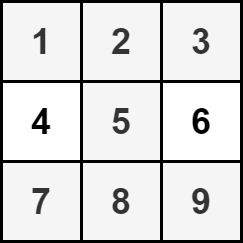
Input: grid = [[1,2,3],[4,5,6],[7,8,9]] Output: 35 Explanation: There is only one hourglass in the matrix, with the sum: 1 + 2 + 3 + 5 + 7 + 8 + 9 = 35.
Constraints:
m == grid.lengthn == grid[i].length3 <= m, n <= 1500 <= grid[i][j] <= 106
Solutions
Solution 1: Enumeration
We observe from the problem statement that each hourglass is a $3 \times 3$ matrix with the first and last elements of the middle row removed. Therefore, we can start from the top left corner, enumerate the middle coordinate $(i, j)$ of each hourglass, then calculate the sum of the elements in the hourglass, and take the maximum value.
The time complexity is $O(m \times n)$, where $m$ and $n$ are the number of rows and columns of the matrix, respectively. The space complexity is $O(1)$.
-
class Solution { public int maxSum(int[][] grid) { int m = grid.length, n = grid[0].length; int ans = 0; for (int i = 1; i < m - 1; ++i) { for (int j = 1; j < n - 1; ++j) { int s = -grid[i][j - 1] - grid[i][j + 1]; for (int x = i - 1; x <= i + 1; ++x) { for (int y = j - 1; y <= j + 1; ++y) { s += grid[x][y]; } } ans = Math.max(ans, s); } } return ans; } } -
class Solution { public: int maxSum(vector<vector<int>>& grid) { int m = grid.size(), n = grid[0].size(); int ans = 0; for (int i = 1; i < m - 1; ++i) { for (int j = 1; j < n - 1; ++j) { int s = -grid[i][j - 1] - grid[i][j + 1]; for (int x = i - 1; x <= i + 1; ++x) { for (int y = j - 1; y <= j + 1; ++y) { s += grid[x][y]; } } ans = max(ans, s); } } return ans; } }; -
class Solution: def maxSum(self, grid: List[List[int]]) -> int: m, n = len(grid), len(grid[0]) ans = 0 for i in range(1, m - 1): for j in range(1, n - 1): s = -grid[i][j - 1] - grid[i][j + 1] s += sum( grid[x][y] for x in range(i - 1, i + 2) for y in range(j - 1, j + 2) ) ans = max(ans, s) return ans -
func maxSum(grid [][]int) (ans int) { m, n := len(grid), len(grid[0]) for i := 1; i < m-1; i++ { for j := 1; j < n-1; j++ { s := -grid[i][j-1] - grid[i][j+1] for x := i - 1; x <= i+1; x++ { for y := j - 1; y <= j+1; y++ { s += grid[x][y] } } ans = max(ans, s) } } return } -
function maxSum(grid: number[][]): number { const m = grid.length; const n = grid[0].length; let ans = 0; for (let i = 1; i < m - 1; ++i) { for (let j = 1; j < n - 1; ++j) { let s = -grid[i][j - 1] - grid[i][j + 1]; for (let x = i - 1; x <= i + 1; ++x) { for (let y = j - 1; y <= j + 1; ++y) { s += grid[x][y]; } } ans = Math.max(ans, s); } } return ans; }