Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2312.html
2312. Selling Pieces of Wood
- Difficulty: Hard.
- Related Topics: Array, Dynamic Programming, Memoization.
- Similar Questions: Tiling a Rectangle with the Fewest Squares, Number of Ways of Cutting a Pizza.
Problem
You are given two integers m and n that represent the height and width of a rectangular piece of wood. You are also given a 2D integer array prices, where prices[i] = [hi, wi, pricei] indicates you can sell a rectangular piece of wood of height hi and width wi for pricei dollars.
To cut a piece of wood, you must make a vertical or horizontal cut across the entire height or width of the piece to split it into two smaller pieces. After cutting a piece of wood into some number of smaller pieces, you can sell pieces according to prices. You may sell multiple pieces of the same shape, and you do not have to sell all the shapes. The grain of the wood makes a difference, so you cannot rotate a piece to swap its height and width.
Return the **maximum money you can earn after cutting an m x n piece of wood**.
Note that you can cut the piece of wood as many times as you want.
Example 1:
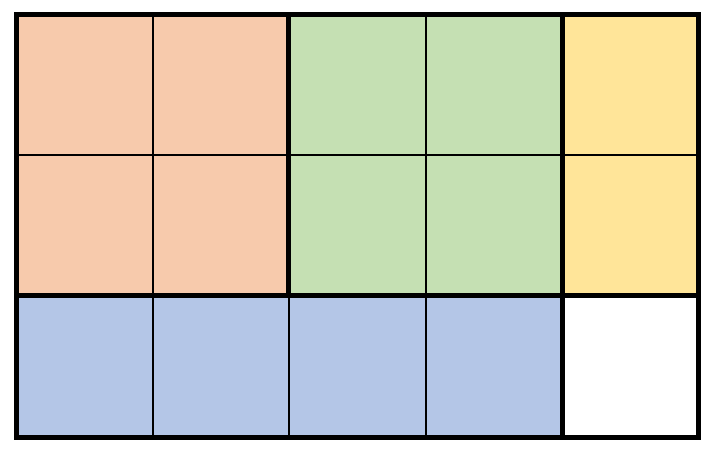
Input: m = 3, n = 5, prices = [[1,4,2],[2,2,7],[2,1,3]]
Output: 19
Explanation: The diagram above shows a possible scenario. It consists of:
- 2 pieces of wood shaped 2 x 2, selling for a price of 2 * 7 = 14.
- 1 piece of wood shaped 2 x 1, selling for a price of 1 * 3 = 3.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 * 2 = 2.
This obtains a total of 14 + 3 + 2 = 19 money earned.
It can be shown that 19 is the maximum amount of money that can be earned.
Example 2:
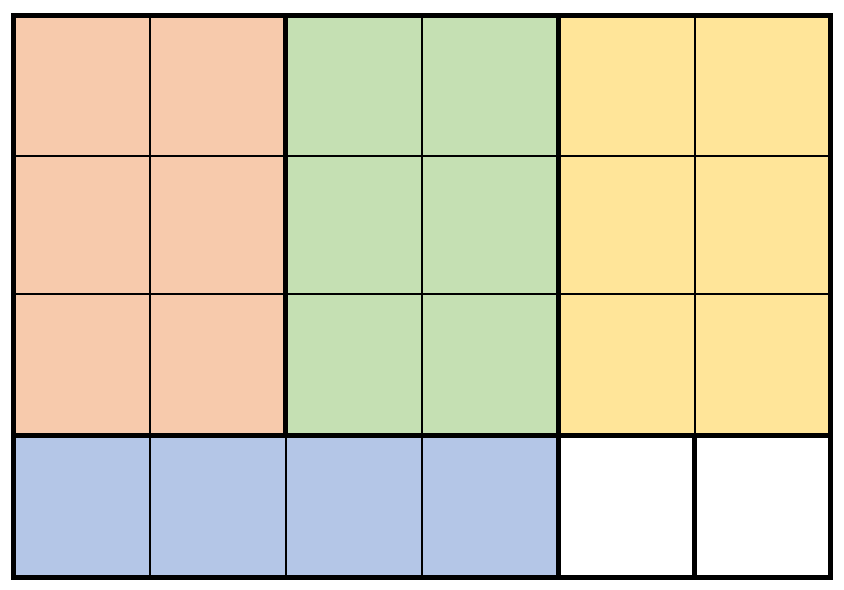
Input: m = 4, n = 6, prices = [[3,2,10],[1,4,2],[4,1,3]]
Output: 32
Explanation: The diagram above shows a possible scenario. It consists of:
- 3 pieces of wood shaped 3 x 2, selling for a price of 3 * 10 = 30.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 * 2 = 2.
This obtains a total of 30 + 2 = 32 money earned.
It can be shown that 32 is the maximum amount of money that can be earned.
Notice that we cannot rotate the 1 x 4 piece of wood to obtain a 4 x 1 piece of wood.
Constraints:
-
1 <= m, n <= 200 -
1 <= prices.length <= 2 * 104 -
prices[i].length == 3 -
1 <= hi <= m -
1 <= wi <= n -
1 <= pricei <= 106 -
All the shapes of wood
(hi, wi)are pairwise distinct.
Solution
-
class Solution { public long sellingWood(int m, int n, int[][] prices) { // dp[i][j] = Maximum profit selling wood of size i*j long[][] dp = new long[m][n]; for (int[] price : prices) { dp[price[0] - 1][price[1] - 1] = Math.max(dp[price[0] - 1][price[1] - 1], price[2]); } for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { // Cut Vertically for (int k = 0; k < j; k++) { dp[i][j] = Math.max(dp[i][j], dp[i][k] + dp[i][j - k - 1]); } // Cut Horizontally for (int k = 0; k < i; k++) { dp[i][j] = Math.max(dp[i][j], dp[k][j] + dp[i - k - 1][j]); } } } return dp[m - 1][n - 1]; } } ############ class Solution { private long[][] memo; private int[][] d; public long sellingWood(int m, int n, int[][] prices) { d = new int[m + 1][n + 1]; memo = new long[m + 1][n + 1]; for (long[] e : memo) { Arrays.fill(e, -1); } for (int[] p : prices) { d[p[0]][p[1]] = p[2]; } return dfs(m, n); } private long dfs(int m, int n) { if (memo[m][n] != -1) { return memo[m][n]; } long ans = d[m][n]; for (int i = 1; i < m / 2 + 1; ++i) { ans = Math.max(ans, dfs(i, n) + dfs(m - i, n)); } for (int i = 1; i < n / 2 + 1; ++i) { ans = Math.max(ans, dfs(m, i) + dfs(m, n - i)); } memo[m][n] = ans; return ans; } } -
class Solution: def sellingWood(self, m: int, n: int, prices: List[List[int]]) -> int: @cache def dfs(h, w): ans = d[h].get(w, 0) for i in range(1, h // 2 + 1): ans = max(ans, dfs(i, w) + dfs(h - i, w)) for i in range(1, w // 2 + 1): ans = max(ans, dfs(h, i) + dfs(h, w - i)) return ans d = defaultdict(dict) for h, w, p in prices: d[h][w] = p return dfs(m, n) ############ # 2312. Selling Pieces of Wood # https://leetcode.com/problems/selling-pieces-of-wood class Solution: def sellingWood(self, m: int, n: int, prices: List[List[int]]) -> int: dp = [[0] * (n + 1) for _ in range(m + 1)] for x, y, price in prices: dp[x][y] = price for w in range(1, m + 1): for h in range(1, n + 1): for a in range(1, w // 2 + 1): dp[w][h] = max(dp[w][h], dp[w - a][h] + dp[a][h]) for b in range(1, h // 2 + 1): dp[w][h] = max(dp[w][h], dp[w][h - b] + dp[w][b]) return dp[m][n] -
using ll = long long; class Solution { public: long long sellingWood(int m, int n, vector<vector<int>>& prices) { vector<vector<ll>> memo(m + 1, vector<ll>(n + 1, -1)); vector<vector<int>> d(m + 1, vector<int>(n + 1)); for (auto& p : prices) d[p[0]][p[1]] = p[2]; return dfs(m, n, d, memo); } ll dfs(int m, int n, vector<vector<int>>& d, vector<vector<ll>>& memo) { if (memo[m][n] != -1) return memo[m][n]; ll ans = d[m][n]; for (int i = 1; i < m / 2 + 1; ++i) ans = max(ans, dfs(i, n, d, memo) + dfs(m - i, n, d, memo)); for (int i = 1; i < n / 2 + 1; ++i) ans = max(ans, dfs(m, i, d, memo) + dfs(m, n - i, d, memo)); memo[m][n] = ans; return ans; } }; -
func sellingWood(m int, n int, prices [][]int) int64 { memo := make([][]int, m+1) d := make([][]int, m+1) for i := range memo { memo[i] = make([]int, n+1) d[i] = make([]int, n+1) for j := range memo[i] { memo[i][j] = -1 } } for _, p := range prices { d[p[0]][p[1]] = p[2] } var dfs func(int, int) int dfs = func(m, n int) int { if memo[m][n] != -1 { return memo[m][n] } ans := d[m][n] for i := 1; i < m/2+1; i++ { ans = max(ans, dfs(i, n)+dfs(m-i, n)) } for i := 1; i < n/2+1; i++ { ans = max(ans, dfs(m, i)+dfs(m, n-i)) } memo[m][n] = ans return ans } return int64(dfs(m, n)) } func max(a, b int) int { if a > b { return a } return b }
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).