Welcome to Subscribe On Youtube
2415. Reverse Odd Levels of Binary Tree
Description
Given the root of a perfect binary tree, reverse the node values at each odd level of the tree.
- For example, suppose the node values at level 3 are
[2,1,3,4,7,11,29,18], then it should become[18,29,11,7,4,3,1,2].
Return the root of the reversed tree.
A binary tree is perfect if all parent nodes have two children and all leaves are on the same level.
The level of a node is the number of edges along the path between it and the root node.
Example 1:
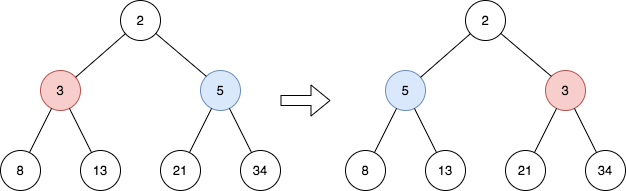
Input: root = [2,3,5,8,13,21,34] Output: [2,5,3,8,13,21,34] Explanation: The tree has only one odd level. The nodes at level 1 are 3, 5 respectively, which are reversed and become 5, 3.
Example 2:

Input: root = [7,13,11] Output: [7,11,13] Explanation: The nodes at level 1 are 13, 11, which are reversed and become 11, 13.
Example 3:
Input: root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2] Output: [0,2,1,0,0,0,0,2,2,2,2,1,1,1,1] Explanation: The odd levels have non-zero values. The nodes at level 1 were 1, 2, and are 2, 1 after the reversal. The nodes at level 3 were 1, 1, 1, 1, 2, 2, 2, 2, and are 2, 2, 2, 2, 1, 1, 1, 1 after the reversal.
Constraints:
- The number of nodes in the tree is in the range
[1, 214]. 0 <= Node.val <= 105rootis a perfect binary tree.
Solutions
Solution 1: BFS
We can use the Breadth-First Search (BFS) method, using a queue $q$ to store the nodes of each level, and a variable $i$ to record the current level. If $i$ is odd, we reverse the values of the nodes at the current level.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the binary tree.
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public TreeNode reverseOddLevels(TreeNode root) { Deque<TreeNode> q = new ArrayDeque<>(); q.offer(root); for (int i = 0; !q.isEmpty(); ++i) { List<TreeNode> t = new ArrayList<>(); for (int k = q.size(); k > 0; --k) { var node = q.poll(); if (i % 2 == 1) { t.add(node); } if (node.left != null) { q.offer(node.left); q.offer(node.right); } } for (int l = 0, r = t.size() - 1; l < r; ++l, --r) { var x = t.get(l).val; t.get(l).val = t.get(r).val; t.get(r).val = x; } } return root; } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: TreeNode* reverseOddLevels(TreeNode* root) { queue<TreeNode*> q{ {root} }; for (int i = 0; q.size(); ++i) { vector<TreeNode*> t; for (int k = q.size(); k; --k) { TreeNode* node = q.front(); q.pop(); if (i & 1) { t.push_back(node); } if (node->left) { q.push(node->left); q.push(node->right); } } for (int l = 0, r = t.size() - 1; l < r; ++l, --r) { swap(t[l]->val, t[r]->val); } } return root; } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def reverseOddLevels(self, root: Optional[TreeNode]) -> Optional[TreeNode]: q = deque([root]) i = 0 while q: if i & 1: l, r = 0, len(q) - 1 while l < r: q[l].val, q[r].val = q[r].val, q[l].val l, r = l + 1, r - 1 for _ in range(len(q)): node = q.popleft() if node.left: q.append(node.left) q.append(node.right) i += 1 return root -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func reverseOddLevels(root *TreeNode) *TreeNode { q := []*TreeNode{root} for i := 0; len(q) > 0; i++ { t := []*TreeNode{} for k := len(q); k > 0; k-- { node := q[0] q = q[1:] if i%2 == 1 { t = append(t, node) } if node.Left != nil { q = append(q, node.Left) q = append(q, node.Right) } } for l, r := 0, len(t)-1; l < r; l, r = l+1, r-1 { t[l].Val, t[r].Val = t[r].Val, t[l].Val } } return root } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function reverseOddLevels(root: TreeNode | null): TreeNode | null { const q: TreeNode[] = [root]; for (let i = 0; q.length > 0; ++i) { if (i % 2) { for (let l = 0, r = q.length - 1; l < r; ++l, --r) { [q[l].val, q[r].val] = [q[r].val, q[l].val]; } } const nq: TreeNode[] = []; for (const { left, right } of q) { if (left) { nq.push(left); nq.push(right); } } q.splice(0, q.length, ...nq); } return root; } -
// Definition for a binary tree node. // #[derive(Debug, PartialEq, Eq)] // pub struct TreeNode { // pub val: i32, // pub left: Option<Rc<RefCell<TreeNode>>>, // pub right: Option<Rc<RefCell<TreeNode>>>, // } // // impl TreeNode { // #[inline] // pub fn new(val: i32) -> Self { // TreeNode { // val, // left: None, // right: None // } // } // } use std::rc::Rc; use std::cell::RefCell; use std::collections::VecDeque; impl Solution { fn create_tree(vals: &Vec<Vec<i32>>, i: usize, j: usize) -> Option<Rc<RefCell<TreeNode>>> { if i == vals.len() { return None; } Some( Rc::new( RefCell::new(TreeNode { val: vals[i][j], left: Self::create_tree(vals, i + 1, j * 2), right: Self::create_tree(vals, i + 1, j * 2 + 1), }) ) ) } pub fn reverse_odd_levels( root: Option<Rc<RefCell<TreeNode>>> ) -> Option<Rc<RefCell<TreeNode>>> { let mut queue = VecDeque::new(); queue.push_back(root); let mut d = 0; let mut vals = Vec::new(); while !queue.is_empty() { let mut val = Vec::new(); for _ in 0..queue.len() { let mut node = queue.pop_front().unwrap(); let mut node = node.as_mut().unwrap().borrow_mut(); val.push(node.val); if node.left.is_some() { queue.push_back(node.left.take()); } if node.right.is_some() { queue.push_back(node.right.take()); } } if d % 2 == 1 { val.reverse(); } vals.push(val); d += 1; } Self::create_tree(&vals, 0, 0) } }