Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2293.html
2293. Min Max Game
- Difficulty: Easy.
- Related Topics: Array, Simulation.
- Similar Questions: Elimination Game, Find Triangular Sum of an Array.
Problem
You are given a 0-indexed integer array nums whose length is a power of 2.
Apply the following algorithm on nums:
-
Let
nbe the length ofnums. Ifn == 1, end the process. Otherwise, create a new 0-indexed integer arraynewNumsof lengthn / 2. -
For every even index
iwhere0 <= i < n / 2, assign the value ofnewNums[i]asmin(nums[2 * i], nums[2 * i + 1]). -
For every odd index
iwhere0 <= i < n / 2, assign the value ofnewNums[i]asmax(nums[2 * i], nums[2 * i + 1]). -
Replace the array
numswithnewNums. -
Repeat the entire process starting from step 1.
Return the last number that remains in **nums after applying the algorithm.**
Example 1:
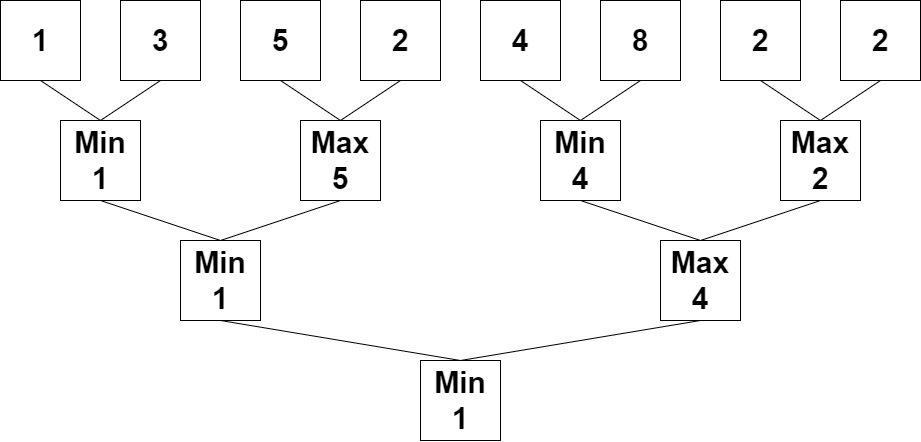
Input: nums = [1,3,5,2,4,8,2,2]
Output: 1
Explanation: The following arrays are the results of applying the algorithm repeatedly.
First: nums = [1,5,4,2]
Second: nums = [1,4]
Third: nums = [1]
1 is the last remaining number, so we return 1.
Example 2:
Input: nums = [3]
Output: 3
Explanation: 3 is already the last remaining number, so we return 3.
Constraints:
-
1 <= nums.length <= 1024 -
1 <= nums[i] <= 109 -
nums.lengthis a power of2.
Solution (Java, C++, Python)
-
class Solution { public int minMaxGame(int[] nums) { int n = nums.length; if (n == 1) { return nums[0]; } int[] newNums = new int[n / 2]; for (int i = 0; i < n / 2; i++) { if (i % 2 == 0) { newNums[i] = Math.min(nums[2 * i], nums[2 * i + 1]); } else { newNums[i] = Math.max(nums[2 * i], nums[2 * i + 1]); } } return minMaxGame(newNums); } } ############ class Solution { public int minMaxGame(int[] nums) { for (int n = nums.length; n > 1;) { n >>= 1; for (int i = 0; i < n; ++i) { int a = nums[i << 1], b = nums[i << 1 | 1]; nums[i] = i % 2 == 0 ? Math.min(a, b) : Math.max(a, b); } } return nums[0]; } } -
class Solution: def minMaxGame(self, nums: List[int]) -> int: n = len(nums) while n > 1: n >>= 1 for i in range(n): a, b = nums[i << 1], nums[i << 1 | 1] nums[i] = min(a, b) if i % 2 == 0 else max(a, b) return nums[0] ############ # 2293. Min Max Game # https://leetcode.com/problems/min-max-game/ class Solution: def minMaxGame(self, nums: List[int]) -> int: while len(nums) != 1: temp = [] for i in range(len(nums) // 2): if i % 2 == 0: temp.append(min(nums[i * 2], nums[i * 2 + 1])) else: temp.append(max(nums[i * 2], nums[i * 2 + 1])) nums = temp return nums[0] -
class Solution { public: int minMaxGame(vector<int>& nums) { for (int n = nums.size(); n > 1;) { n >>= 1; for (int i = 0; i < n; ++i) { int a = nums[i << 1], b = nums[i << 1 | 1]; nums[i] = i % 2 == 0 ? min(a, b) : max(a, b); } } return nums[0]; } }; -
func minMaxGame(nums []int) int { for n := len(nums); n > 1; { n >>= 1 for i := 0; i < n; i++ { a, b := nums[i<<1], nums[i<<1|1] if i%2 == 0 { nums[i] = min(a, b) } else { nums[i] = max(a, b) } } } return nums[0] } func min(a, b int) int { if a < b { return a } return b } func max(a, b int) int { if a > b { return a } return b } -
function minMaxGame(nums: number[]): number { for (let n = nums.length; n > 1; ) { n >>= 1; for (let i = 0; i < n; ++i) { const a = nums[i << 1]; const b = nums[(i << 1) | 1]; nums[i] = i % 2 == 0 ? Math.min(a, b) : Math.max(a, b); } } return nums[0]; } -
impl Solution { pub fn min_max_game(mut nums: Vec<i32>) -> i32 { let mut n = nums.len(); while n != 1 { n >>= 1; for i in 0..n { nums[i] = (if i & 1 == 1 { i32::max } else { i32::min })(nums[i << 1], nums[i << 1 | 1]) } } nums[0] } }
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).