Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2290.html
2290. Minimum Obstacle Removal to Reach Corner
- Difficulty: Hard.
- Related Topics: Array, Breadth-First Search, Graph, Heap (Priority Queue), Matrix, Shortest Path.
- Similar Questions: Shortest Path in a Grid with Obstacles Elimination.
Problem
You are given a 0-indexed 2D integer array grid of size m x n. Each cell has one of two values:
-
0represents an empty cell, -
1represents an obstacle that may be removed.
You can move up, down, left, or right from and to an empty cell.
Return the **minimum number of obstacles to remove so you can move from the upper left corner (0, 0) to the lower right corner **(m - 1, n - 1).
Example 1:
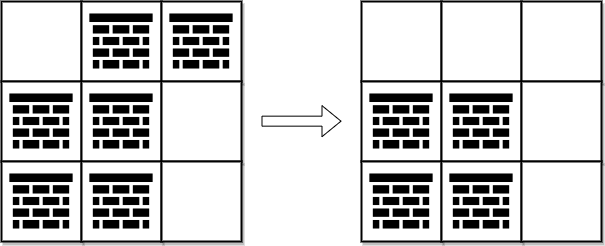
Input: grid = [[0,1,1],[1,1,0],[1,1,0]]
Output: 2
Explanation: We can remove the obstacles at (0, 1) and (0, 2) to create a path from (0, 0) to (2, 2).
It can be shown that we need to remove at least 2 obstacles, so we return 2.
Note that there may be other ways to remove 2 obstacles to create a path.
Example 2:
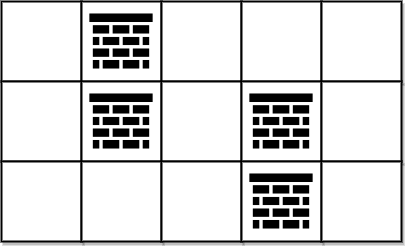
Input: grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]
Output: 0
Explanation: We can move from (0, 0) to (2, 4) without removing any obstacles, so we return 0.
Constraints:
-
m == grid.length -
n == grid[i].length -
1 <= m, n <= 105 -
2 <= m * n <= 105 -
grid[i][j]is either0or1. -
grid[0][0] == grid[m - 1][n - 1] == 0
Solution
-
class Solution { public int minimumObstacles(int[][] grid) { int n = grid.length; int m = grid[0].length; int[][] dirs = new int[][] { {0, 1}, {1, 0}, {0, -1}, {-1, 0} }; Queue<State> q = new PriorityQueue<>((a, b) -> a.removed - b.removed); q.add(new State(0, 0, 0)); boolean[][] visited = new boolean[n][m]; visited[0][0] = true; while (!q.isEmpty()) { State state = q.poll(); if (state.r == n - 1 && state.c == m - 1) { return state.removed; } for (int[] d : dirs) { int nr = state.r + d[0]; int nc = state.c + d[1]; if (nr < 0 || nc < 0 || nr == n || nc == m || visited[nr][nc]) { continue; } visited[nr][nc] = true; State next = new State(nr, nc, state.removed); if (grid[nr][nc] == 1) { next.removed++; } q.add(next); } } return -1; } private static class State { int r; int c; int removed; State(int r, int c, int removed) { this.r = r; this.c = c; this.removed = removed; } } } ############ class Solution { public int minimumObstacles(int[][] grid) { int m = grid.length, n = grid[0].length; Deque<int[]> q = new ArrayDeque<>(); q.offer(new int[] {0, 0, 0}); int[] dirs = {-1, 0, 1, 0, -1}; boolean[][] vis = new boolean[m][n]; while (true) { var p = q.poll(); int i = p[0], j = p[1], k = p[2]; if (i == m - 1 && j == n - 1) { return k; } if (vis[i][j]) { continue; } vis[i][j] = true; for (int h = 0; h < 4; ++h) { int x = i + dirs[h], y = j + dirs[h + 1]; if (x >= 0 && x < m && y >= 0 && y < n) { if (grid[x][y] == 0) { q.offerFirst(new int[] {x, y, k}); } else { q.offerLast(new int[] {x, y, k + 1}); } } } } } } -
class Solution: def minimumObstacles(self, grid: List[List[int]]) -> int: m, n = len(grid), len(grid[0]) q = deque([(0, 0, 0)]) vis = set() dirs = (-1, 0, 1, 0, -1) while 1: i, j, k = q.popleft() if i == m - 1 and j == n - 1: return k if (i, j) in vis: continue vis.add((i, j)) for a, b in pairwise(dirs): x, y = i + a, j + b if 0 <= x < m and 0 <= y < n: if grid[x][y] == 0: q.appendleft((x, y, k)) else: q.append((x, y, k + 1)) ############ # 2290. Minimum Obstacle Removal to Reach Corner # https://leetcode.com/problems/minimum-obstacle-removal-to-reach-corner class Solution: def minimumObstacles(self, grid: List[List[int]]) -> int: rows, cols = len(grid), len(grid[0]) dist = [[float('inf')] * cols for _ in range(rows)] dist[0][0] = 0 heap = [(0, 0, 0)] while heap: k, x, y = heappop(heap) if dist[x][y] != k: continue for dx, dy in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]: if 0 <= dx < rows and 0 <= dy < cols: old = dist[dx][dy] new = k + grid[dx][dy] if new < old: dist[dx][dy] = new heappush(heap, (new, dx, dy)) return dist[-1][-1] -
class Solution { public: int minimumObstacles(vector<vector<int>>& grid) { int m = grid.size(), n = grid[0].size(); deque<tuple<int, int, int>> q{ {0, 0, 0} }; bool vis[m][n]; memset(vis, 0, sizeof vis); int dirs[5] = {-1, 0, 1, 0, -1}; while (1) { auto [i, j, k] = q.front(); q.pop_front(); if (i == m - 1 && j == n - 1) { return k; } if (vis[i][j]) { continue; } vis[i][j] = true; for (int h = 0; h < 4; ++h) { int x = i + dirs[h], y = j + dirs[h + 1]; if (x >= 0 && x < m && y >= 0 && y < n) { if (grid[x][y] == 0) { q.push_front({x, y, k}); } else { q.push_back({x, y, k + 1}); } } } } } }; -
func minimumObstacles(grid [][]int) int { m, n := len(grid), len(grid[0]) q := doublylinkedlist.New() type tuple struct{ i, j, k int } q.Add(tuple{0, 0, 0}) vis := make([][]bool, m) for i := range vis { vis[i] = make([]bool, n) } dirs := [5]int{-1, 0, 1, 0, -1} for { v, _ := q.Get(0) p := v.(tuple) q.Remove(0) i, j, k := p.i, p.j, p.k if i == m-1 && j == n-1 { return k } if vis[i][j] { continue } vis[i][j] = true for h := 0; h < 4; h++ { x, y := i+dirs[h], j+dirs[h+1] if x >= 0 && x < m && y >= 0 && y < n { if grid[x][y] == 0 { q.Insert(0, tuple{x, y, k}) } else { q.Add(tuple{x, y, k + 1}) } } } } } -
function minimumObstacles(grid: number[][]): number { const m = grid.length, n = grid[0].length; const dirs = [ [0, 1], [0, -1], [1, 0], [-1, 0], ]; let ans = Array.from({ length: m }, v => new Array(n).fill(Infinity)); ans[0][0] = 0; let deque = [[0, 0]]; while (deque.length) { let [x, y] = deque.shift(); for (let [dx, dy] of dirs) { let [i, j] = [x + dx, y + dy]; if (i < 0 || i > m - 1 || j < 0 || j > n - 1) continue; const cost = grid[i][j]; if (ans[x][y] + cost >= ans[i][j]) continue; ans[i][j] = ans[x][y] + cost; deque.push([i, j]); } } return ans[m - 1][n - 1]; }
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).