Welcome to Subscribe On Youtube

Formatted question description: https://leetcode.ca/all/2285.html

2285. Maximum Total Importance of Roads

• Difficulty: Medium.
• Related Topics: Greedy, Graph, Sorting, Heap (Priority Queue).
• Similar Questions: .

Problem

You are given an integer n denoting the number of cities in a country. The cities are numbered from 0 to n - 1.

You are also given a 2D integer array roads where roads[i] = [ai, bi] denotes that there exists a bidirectional road connecting cities ai and bi.

You need to assign each city with an integer value from 1 to n, where each value can only be used once. The importance of a road is then defined as the sum of the values of the two cities it connects.

Return the **maximum total importance of all roads possible after assigning the values optimally.**

  Example 1:

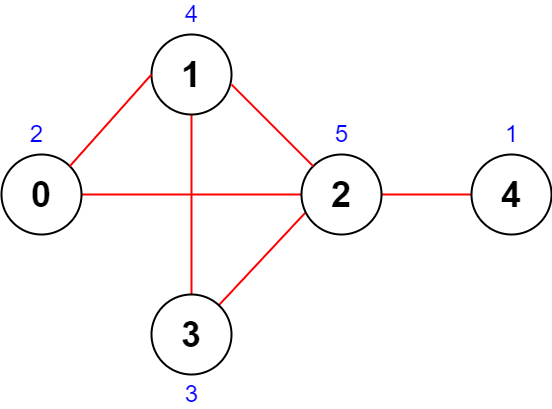
Input: n = 5, roads = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
Output: 43
Explanation: The figure above shows the country and the assigned values of [2,4,5,3,1].
- The road (0,1) has an importance of 2 + 4 = 6.
- The road (1,2) has an importance of 4 + 5 = 9.
- The road (2,3) has an importance of 5 + 3 = 8.
- The road (0,2) has an importance of 2 + 5 = 7.
- The road (1,3) has an importance of 4 + 3 = 7.
- The road (2,4) has an importance of 5 + 1 = 6.
The total importance of all roads is 6 + 9 + 8 + 7 + 7 + 6 = 43.
It can be shown that we cannot obtain a greater total importance than 43.

Example 2:

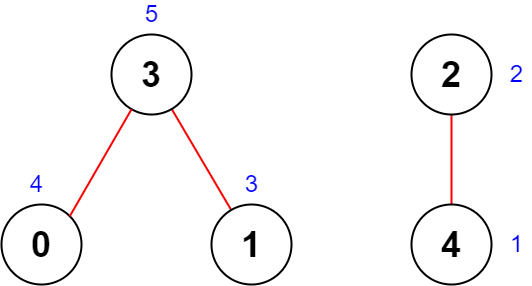
Input: n = 5, roads = [[0,3],[2,4],[1,3]]
Output: 20
Explanation: The figure above shows the country and the assigned values of [4,3,2,5,1].
- The road (0,3) has an importance of 4 + 5 = 9.
- The road (2,4) has an importance of 2 + 1 = 3.
- The road (1,3) has an importance of 3 + 5 = 8.
The total importance of all roads is 9 + 3 + 8 = 20.
It can be shown that we cannot obtain a greater total importance than 20.

  Constraints:

• 2 <= n <= 5 * 104

• 1 <= roads.length <= 5 * 104

• roads[i].length == 2

• 0 <= ai, bi <= n - 1

• ai != bi

• There are no duplicate roads.

Solution (Java, C++, Python)

• Java
• Python
• C++
• Go

• class Solution {
      public long maximumImportance(int n, int[][] roads) {
          int[] degree = new int[n];
          int maxdegree = 0;
          for (int[] r : roads) {
              degree[r[0]]++;
              degree[r[1]]++;
              maxdegree = Math.max(maxdegree, Math.max(degree[r[0]], degree[r[1]]));
          }
          Map<Integer, Integer> rank = new HashMap<>();
          int i = n;
          while (i > 0) {
              for (int j = 0; j < n; j++) {
                  if (degree[j] == maxdegree) {
                      rank.put(j, i--);
                      degree[j] = Integer.MIN_VALUE;
                  }
              }
              maxdegree = 0;
              for (int d : degree) {
                  maxdegree = Math.max(maxdegree, d);
              }
          }
          long res = 0;
          for (int[] r : roads) {
              res += rank.get(r[0]) + rank.get(r[1]);
          }
          return res;
      }
  }
  
  ############
  
  class Solution {
      public long maximumImportance(int n, int[][] roads) {
          int[] deg = new int[n];
          for (int[] r : roads) {
              ++deg[r[0]];
              ++deg[r[1]];
          }
          Arrays.sort(deg);
          long ans = 0;
          for (int i = 0; i < n; ++i) {
              ans += (long) (i + 1) * deg[i];
          }
          return ans;
      }
  }
  

• class Solution:
      def maximumImportance(self, n: int, roads: List[List[int]]) -> int:
          deg = [0] * n
          for a, b in roads:
              deg[a] += 1
              deg[b] += 1
          deg.sort()
          return sum(i * v for i, v in enumerate(deg, 1))
  
  ############
  
  # 2285. Maximum Total Importance of Roads
  # https://leetcode.com/problems/maximum-total-importance-of-roads/
  
  class Solution:
      def maximumImportance(self, n: int, roads: List[List[int]]) -> int:
          count = defaultdict(int)
  
          for a, b in roads:
              count[a] += 1
              count[b] += 1
  
          scores = defaultdict(int)
          
          v = sorted(count.items(), key = lambda x:-x[1])
          
          for k, cnt in v:
              scores[k] = n
              n -= 1
          
          res = 0
          
          for a, b in roads:
              res += scores[a] + scores[b]
          
          return res
  
  

• class Solution {
  public:
      long long maximumImportance(int n, vector<vector<int>>& roads) {
          vector<int> deg(n);
          for (auto& r : roads) {
              ++deg[r[0]];
              ++deg[r[1]];
          }
          sort(deg.begin(), deg.end());
          long long ans = 0;
          for (int i = 0; i < n; ++i) ans += 1ll * (i + 1) * deg[i];
          return ans;
      }
  };
  

• func maximumImportance(n int, roads [][]int) int64 {
  	deg := make([]int, n)
  	for _, r := range roads {
  		deg[r[0]]++
  		deg[r[1]]++
  	}
  	sort.Ints(deg)
  	var ans int64
  	for i := 0; i < n; i++ {
  		ans += int64((i + 1) * deg[i])
  	}
  	return ans
  }
  

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).

All Problems

All Solutions