Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2242.html
2242. Maximum Score of a Node Sequence
- Difficulty: Hard.
- Related Topics: Array, Graph, Sorting, Enumeration.
- Similar Questions: Get the Maximum Score.
Problem
There is an undirected graph with n nodes, numbered from 0 to n - 1.
You are given a 0-indexed integer array scores of length n where scores[i] denotes the score of node i. You are also given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.
A node sequence is valid if it meets the following conditions:
-
There is an edge connecting every pair of adjacent nodes in the sequence.
-
No node appears more than once in the sequence.
The score of a node sequence is defined as the sum of the scores of the nodes in the sequence.
Return the **maximum score of a valid node sequence with a length of 4. If no such sequence exists, return **-1.
Example 1:
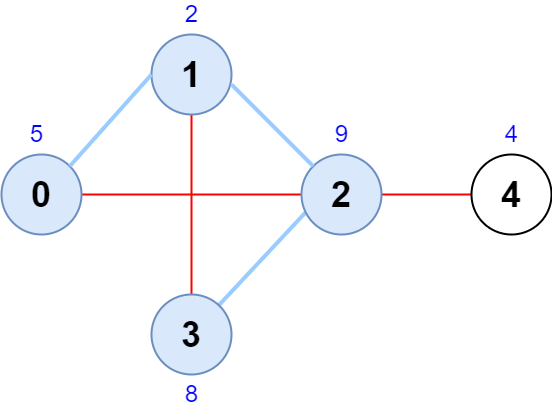
Input: scores = [5,2,9,8,4], edges = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
Output: 24
Explanation: The figure above shows the graph and the chosen node sequence [0,1,2,3].
The score of the node sequence is 5 + 2 + 9 + 8 = 24.
It can be shown that no other node sequence has a score of more than 24.
Note that the sequences [3,1,2,0] and [1,0,2,3] are also valid and have a score of 24.
The sequence [0,3,2,4] is not valid since no edge connects nodes 0 and 3.
Example 2:
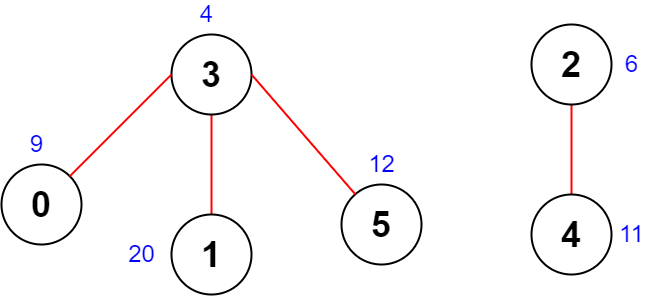
Input: scores = [9,20,6,4,11,12], edges = [[0,3],[5,3],[2,4],[1,3]]
Output: -1
Explanation: The figure above shows the graph.
There are no valid node sequences of length 4, so we return -1.
Constraints:
-
n == scores.length -
4 <= n <= 5 * 104 -
1 <= scores[i] <= 108 -
0 <= edges.length <= 5 * 104 -
edges[i].length == 2 -
0 <= ai, bi <= n - 1 -
ai != bi -
There are no duplicate edges.
Solution
-
class Solution { public int maximumScore(int[] scores, int[][] edges) { // store only top 3 nodes (having highest scores) int[][] graph = new int[scores.length][3]; for (int[] a : graph) { Arrays.fill(a, -1); } for (int[] edge : edges) { insert(edge[0], graph[edge[1]], scores); insert(edge[1], graph[edge[0]], scores); } int maxScore = -1; for (int[] edge : edges) { int u = edge[0]; int v = edge[1]; int score = scores[u] + scores[v]; for (int i = 0; i < 3; i++) { // if neighbour is current node, skip if (graph[u][i] == -1 || graph[u][i] == v) { continue; } for (int j = 0; j < 3; j++) { // if neighbour is current node or already choosen node, skip if (graph[v][j] == -1 || graph[v][j] == u) { continue; } if (graph[v][j] == graph[u][i]) { continue; } maxScore = Math.max(maxScore, score + scores[graph[u][i]] + scores[graph[v][j]]); } } } return maxScore; } private void insert(int n, int[] arr, int[] scores) { if (arr[0] == -1) { arr[0] = n; } else if (arr[1] == -1) { if (scores[arr[0]] < scores[n]) { arr[1] = arr[0]; arr[0] = n; } else { arr[1] = n; } } else if (arr[2] == -1) { if (scores[arr[0]] < scores[n]) { arr[2] = arr[1]; arr[1] = arr[0]; arr[0] = n; } else if (scores[arr[1]] < scores[n]) { arr[2] = arr[1]; arr[1] = n; } else { arr[2] = n; } } else { if (scores[arr[1]] < scores[n]) { arr[2] = arr[1]; arr[1] = n; } else if (scores[arr[2]] < scores[n]) { arr[2] = n; } } } } ############ class Solution { public int maximumScore(int[] scores, int[][] edges) { int n = scores.length; List<Integer>[] g = new List[n]; Arrays.setAll(g, k -> new ArrayList<>()); for (int[] e : edges) { int a = e[0], b = e[1]; g[a].add(b); g[b].add(a); } for (int i = 0; i < n; ++i) { g[i].sort((a, b) -> scores[b] - scores[a]); g[i] = g[i].subList(0, Math.min(3, g[i].size())); } int ans = -1; for (int[] e : edges) { int a = e[0], b = e[1]; for (int c : g[a]) { for (int d : g[b]) { if (c != b && c != d && a != d) { int t = scores[a] + scores[b] + scores[c] + scores[d]; ans = Math.max(ans, t); } } } } return ans; } } -
class Solution: def maximumScore(self, scores: List[int], edges: List[List[int]]) -> int: g = defaultdict(list) for a, b in edges: g[a].append(b) g[b].append(a) for k in g.keys(): g[k] = nlargest(3, g[k], key=lambda x: scores[x]) ans = -1 for a, b in edges: for c in g[a]: for d in g[b]: if b != c != d != a: t = scores[a] + scores[b] + scores[c] + scores[d] ans = max(ans, t) return ans ############ # 2242. Maximum Score of a Node Sequence # https://leetcode.com/problems/maximum-score-of-a-node-sequence/ class Solution: def maximumScore(self, scores: List[int], edges: List[List[int]]) -> int: d = defaultdict(list) def go(x, y): if len(d[x]) == 3: heapq.heappushpop(d[x], (scores[y], y)) else: heapq.heappush(d[x], (scores[y], y)) for x, y in edges: go(x, y) go(y, x) res = float('-inf') for x, y in edges: for score1, node1 in d[x]: for score2, node2 in d[y]: if node1 not in (x, y) and node2 not in (x, y) and node1 != node2: res = max(res, scores[x] + scores[y] + score1 + score2) return -1 if res == float('-inf') else res
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).