Welcome to Subscribe On Youtube
2319. Check if Matrix Is X-Matrix
Description
A square matrix is said to be an X-Matrix if both of the following conditions hold:
- All the elements in the diagonals of the matrix are non-zero.
- All other elements are 0.
Given a 2D integer array grid of size n x n representing a square matrix, return true if grid is an X-Matrix. Otherwise, return false.
Example 1:
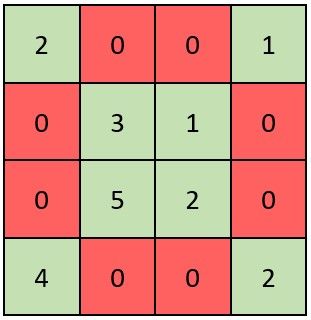
Input: grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]] Output: true Explanation: Refer to the diagram above. An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0. Thus, grid is an X-Matrix.
Example 2:
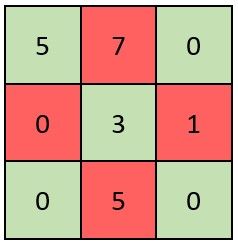
Input: grid = [[5,7,0],[0,3,1],[0,5,0]] Output: false Explanation: Refer to the diagram above. An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0. Thus, grid is not an X-Matrix.
Constraints:
n == grid.length == grid[i].length3 <= n <= 1000 <= grid[i][j] <= 105
Solutions
-
class Solution { public boolean checkXMatrix(int[][] grid) { int n = grid.length; for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { if (i == j || i + j == n - 1) { if (grid[i][j] == 0) { return false; } } else if (grid[i][j] != 0) { return false; } } } return true; } } -
class Solution { public: bool checkXMatrix(vector<vector<int>>& grid) { int n = grid.size(); for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { if (i == j || i + j == n - 1) { if (!grid[i][j]) { return false; } } else if (grid[i][j]) { return false; } } } return true; } }; -
class Solution: def checkXMatrix(self, grid: List[List[int]]) -> bool: for i, row in enumerate(grid): for j, v in enumerate(row): if i == j or i + j == len(grid) - 1: if v == 0: return False elif v: return False return True -
func checkXMatrix(grid [][]int) bool { for i, row := range grid { for j, v := range row { if i == j || i+j == len(row)-1 { if v == 0 { return false } } else if v != 0 { return false } } } return true } -
function checkXMatrix(grid: number[][]): boolean { const n = grid.length; for (let i = 0; i < n; ++i) { for (let j = 0; j < n; ++j) { if (i == j || i + j == n - 1) { if (!grid[i][j]) { return false; } } else if (grid[i][j]) { return false; } } } return true; } -
public class Solution { public bool CheckXMatrix(int[][] grid) { int n = grid.Length; for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { if (i == j || i + j == n - 1) { if (grid[i][j] == 0) { return false; } } else if (grid[i][j] != 0) { return false; } } } return true; } } -
impl Solution { pub fn check_x_matrix(grid: Vec<Vec<i32>>) -> bool { let n = grid.len(); for i in 0..n { for j in 0..n { if i == j || i + j == n - 1 { if grid[i][j] == 0 { return false; } } else if grid[i][j] != 0 { return false; } } } true } }