2316. Count Unreachable Pairs of Nodes in an Undirected Graph

Description

You are given an integer n. There is an undirected graph with n nodes, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [a_i, b_i] denotes that there exists an undirected edge connecting nodes a_i and b_i.

Return the number of pairs of different nodes that are unreachable from each other.

Example 1:

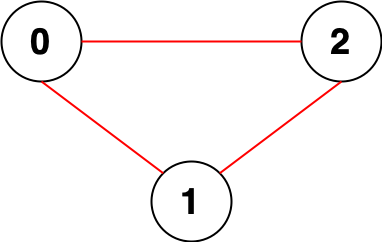
Input: n = 3, edges = [[0,1],[0,2],[1,2]]
Output: 0
Explanation: There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.

Example 2:

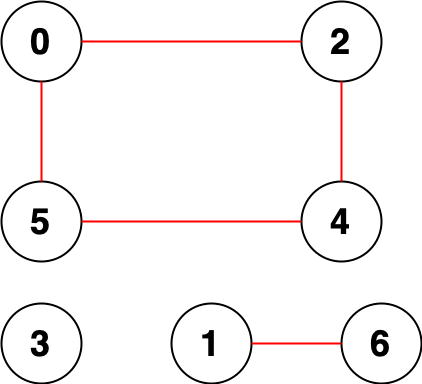
Input: n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
Output: 14
Explanation: There are 14 pairs of nodes that are unreachable from each other:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]].
Therefore, we return 14.

Constraints:

1 <= n <= 10⁵
0 <= edges.length <= 2 * 10⁵
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
There are no repeated edges.

Solutions

Solution 1: DFS

For any two nodes in an undirected graph, if there is a path between them, then they are mutually reachable.

Therefore, we can use depth-first search to find the number of nodes $t$ in each connected component, and then multiply the current number of nodes $t$ in the connected component by the number of nodes $s$ in all previous connected components to obtain the number of unreachable node pairs in the current connected component, which is $s \times t$. Then, we add $t$ to $s$ and continue to search for the next connected component until all connected components have been searched, and we can obtain the final answer.

The time complexity is $O(n + m)$, and the space complexity is $O(n + m)$. Here, $n$ and $m$ are the number of nodes and edges, respectively.

class Solution {
    private List<Integer>[] g;
    private boolean[] vis;

    public long countPairs(int n, int[][] edges) {
        g = new List[n];
        vis = new boolean[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        long ans = 0, s = 0;
        for (int i = 0; i < n; ++i) {
            int t = dfs(i);
            ans += s * t;
            s += t;
        }
        return ans;
    }

    private int dfs(int i) {
        if (vis[i]) {
            return 0;
        }
        vis[i] = true;
        int cnt = 1;
        for (int j : g[i]) {
            cnt += dfs(j);
        }
        return cnt;
    }
}

class Solution {
public:
    long long countPairs(int n, vector<vector<int>>& edges) {
        vector<int> g[n];
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        bool vis[n];
        memset(vis, 0, sizeof(vis));
        function<int(int)> dfs = [&](int i) {
            if (vis[i]) {
                return 0;
            }
            vis[i] = true;
            int cnt = 1;
            for (int j : g[i]) {
                cnt += dfs(j);
            }
            return cnt;
        };
        long long ans = 0, s = 0;
        for (int i = 0; i < n; ++i) {
            int t = dfs(i);
            ans += s * t;
            s += t;
        }
        return ans;
    }
};

class Solution:
    def countPairs(self, n: int, edges: List[List[int]]) -> int:
        def dfs(i: int) -> int:
            if vis[i]:
                return 0
            vis[i] = True
            return 1 + sum(dfs(j) for j in g[i])

        g = [[] for _ in range(n)]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        vis = [False] * n
        ans = s = 0
        for i in range(n):
            t = dfs(i)
            ans += s * t
            s += t
        return ans

func countPairs(n int, edges [][]int) (ans int64) {
	g := make([][]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	vis := make([]bool, n)
	var dfs func(int) int
	dfs = func(i int) int {
		if vis[i] {
			return 0
		}
		vis[i] = true
		cnt := 1
		for _, j := range g[i] {
			cnt += dfs(j)
		}
		return cnt
	}
	var s int64
	for i := 0; i < n; i++ {
		t := int64(dfs(i))
		ans += s * t
		s += t
	}
	return
}

function countPairs(n: number, edges: number[][]): number {
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    const vis: boolean[] = Array(n).fill(false);
    const dfs = (i: number): number => {
        if (vis[i]) {
            return 0;
        }
        vis[i] = true;
        let cnt = 1;
        for (const j of g[i]) {
            cnt += dfs(j);
        }
        return cnt;
    };
    let [ans, s] = [0, 0];
    for (let i = 0; i < n; ++i) {
        const t = dfs(i);
        ans += s * t;
        s += t;
    }
    return ans;
}

impl Solution {
    pub fn count_pairs(n: i32, edges: Vec<Vec<i32>>) -> i64 {
        let n = n as usize;
        let mut g = vec![vec![]; n];
        let mut vis = vec![false; n];
        for e in edges {
            let u = e[0] as usize;
            let v = e[1] as usize;
            g[u].push(v);
            g[v].push(u);
        }

        fn dfs(g: &Vec<Vec<usize>>, vis: &mut Vec<bool>, u: usize) -> i64 {
            if vis[u] {
                return 0;
            }
            vis[u] = true;
            let mut cnt = 1;
            for &v in &g[u] {
                cnt += dfs(g, vis, v);
            }
            cnt
        }

        let mut ans = 0;
        let mut s = 0;
        for u in 0..n {
            let t = dfs(&g, &mut vis, u);
            ans += t * s;
            s += t;
        }
        ans
    }
}

2316 - Count Unreachable Pairs of Nodes in an Undirected Graph

2316. Count Unreachable Pairs of Nodes in an Undirected Graph

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

2316. Count Unreachable Pairs of Nodes in an Undirected Graph

Description

Solutions

All Problems

All Solutions