Formatted question description: https://leetcode.ca/all/2146.html

2146. K Highest Ranked Items Within a Price Range (Medium)

You are given a 0-indexed 2D integer array grid of size m x n that represents a map of the items in a shop. The integers in the grid represent the following:

0 represents a wall that you cannot pass through.
1 represents an empty cell that you can freely move to and from.
All other positive integers represent the price of an item in that cell. You may also freely move to and from these item cells.

It takes 1 step to travel between adjacent grid cells.

You are also given integer arrays pricing and start where pricing = [low, high] and start = [row, col] indicates that you start at the position (row, col) and are interested only in items with a price in the range of [low, high] (inclusive). You are further given an integer k.

You are interested in the positions of the k highest-ranked items whose prices are within the given price range. The rank is determined by the first of these criteria that is different:

Distance, defined as the length of the shortest path from the start (shorter distance has a higher rank).
Price (lower price has a higher rank, but it must be in the price range).
The row number (smaller row number has a higher rank).
The column number (smaller column number has a higher rank).

Return the k highest-ranked items within the price range sorted by their rank (highest to lowest). If there are fewer than k reachable items within the price range, return all of them.

Example 1:

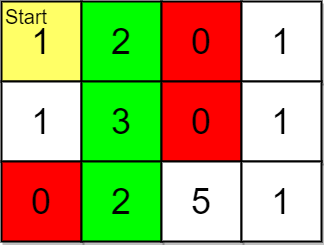
Input: grid = [[1,2,0,1],[1,3,0,1],[0,2,5,1]], pricing = [2,5], start = [0,0], k = 3
Output: [[0,1],[1,1],[2,1]]
Explanation: You start at (0,0).
With a price range of [2,5], we can take items from (0,1), (1,1), (2,1) and (2,2).
The ranks of these items are:
- (0,1) with distance 1
- (1,1) with distance 2
- (2,1) with distance 3
- (2,2) with distance 4
Thus, the 3 highest ranked items in the price range are (0,1), (1,1), and (2,1).

Example 2:

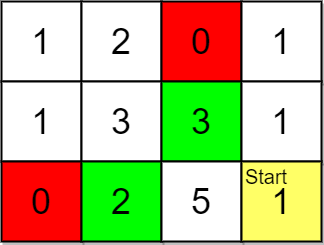
Input: grid = [[1,2,0,1],[1,3,3,1],[0,2,5,1]], pricing = [2,3], start = [2,3], k = 2
Output: [[2,1],[1,2]]
Explanation: You start at (2,3).
With a price range of [2,3], we can take items from (0,1), (1,1), (1,2) and (2,1).
The ranks of these items are:
- (2,1) with distance 2, price 2
- (1,2) with distance 2, price 3
- (1,1) with distance 3
- (0,1) with distance 4
Thus, the 2 highest ranked items in the price range are (2,1) and (1,2).

Example 3:

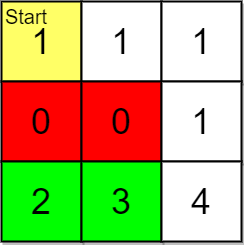
Input: grid = [[1,1,1],[0,0,1],[2,3,4]], pricing = [2,3], start = [0,0], k = 3
Output: [[2,1],[2,0]]
Explanation: You start at (0,0).
With a price range of [2,3], we can take items from (2,0) and (2,1). 
The ranks of these items are: 
- (2,1) with distance 5
- (2,0) with distance 6
Thus, the 2 highest ranked items in the price range are (2,1) and (2,0). 
Note that k = 3 but there are only 2 reachable items within the price range.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 10⁵
1 <= m * n <= 10⁵
0 <= grid[i][j] <= 10⁵
pricing.length == 2
2 <= low <= high <= 10⁵
start.length == 2
0 <= row <= m - 1
0 <= col <= n - 1
grid[row][col] > 0
1 <= k <= m * n

Similar Questions:

Solution 1. BFS + Sorting

BFS to visit all the cells reachable. If the price of the cell is within the range, add this cell into the answer array.

Sort the answer array using the criteria specified, and only keep the first k cells.

// OJ: https://leetcode.com/problems/k-highest-ranked-items-within-a-price-range/
// Time: O(MNlog(MN))
// Space: O(MN)
class Solution {
public:
    vector<vector<int>> highestRankedKItems(vector<vector<int>>& A, vector<int>& P, vector<int>& start, int k) {
        int M = A.size(), N = A[0].size(), step = 0, dirs[4][2] = { {0,1},{0,-1},{1,0},{-1,0} };
        queue<pair<int, int>> q{ { {start[0], start[1]} } };
        vector<vector<int>> dist(M, vector<int>(N, INT_MAX)), ans; // dist[x][y] is the shortest distance from (x,y) to `start`.
        dist[start[0]][start[1]] = 0;
        while (q.size()) {
            int cnt = q.size();
            while (cnt--) {
                auto [x, y] = q.front();
                q.pop();
                if (A[x][y] >= P[0] && A[x][y] <= P[1]) ans.push_back({x, y});
                for (auto &[dx, dy] : dirs) {
                    int a = x + dx, b = y + dy;
                    if (a < 0 || b < 0 || a >= M || b >= N || A[a][b] == 0 || dist[a][b] != INT_MAX) continue;
                    dist[a][b] = step + 1;
                    q.emplace(a, b);
                }
            }
            ++step;
        }
        sort(begin(ans), end(ans), [&](auto &a, auto &b) {
            int x1 = a[0], y1 = a[1], x2 = b[0], y2 = b[1];
            int d1 = dist[x1][y1], d2 = dist[x2][y2];
            if (d1 != d2) return d1 < d2;
            int p1 = A[x1][y1], p2 = A[x2][y2];
            if (p1 != p2) return p1 < p2;
            return a < b;
        });
        if (ans.size() > k) ans.resize(k);
        return ans;
    }
};

class Solution:
    def highestRankedKItems(
        self, grid: List[List[int]], pricing: List[int], start: List[int], k: int
    ) -> List[List[int]]:
        m, n = len(grid), len(grid[0])
        row, col, low, high = start + pricing
        items = []
        if low <= grid[row][col] <= high:
            items.append([0, grid[row][col], row, col])
        q = deque([(row, col, 0)])
        grid[row][col] = 0
        while q:
            i, j, d = q.popleft()
            for a, b in [[0, 1], [0, -1], [1, 0], [-1, 0]]:
                x, y = i + a, j + b
                if 0 <= x < m and 0 <= y < n and grid[x][y]:
                    if low <= grid[x][y] <= high:
                        items.append([d + 1, grid[x][y], x, y])
                    q.append((x, y, d + 1))
                    grid[x][y] = 0
        items.sort()
        return [item[2:] for item in items][:k]

############

# 2146. K Highest Ranked Items Within a Price Range
# https://leetcode.com/problems/k-highest-ranked-items-within-a-price-range/

class Solution:
    def highestRankedKItems(self, grid: List[List[int]], pricing: List[int], start: List[int], k: int) -> List[List[int]]:
        rows, cols = len(grid), len(grid[0])
        heap = []
        sx, sy = start
        minP, maxP = pricing
        queue = deque([(sx, sy, 0)])
        visited = set([(sx, sy)])
        
        while queue:
            x, y, distance = queue.popleft()
            
            price = grid[x][y]

            if price != 1 and minP <= price <= maxP:
                if len(heap) == k:
                    heapq.heappushpop(heap, (-distance, -price, -x, -y))
                else:
                    heapq.heappush(heap, (-distance, -price, -x, -y))

            for dx, dy in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]:
                if 0 <= dx < rows and 0 <= dy < cols and grid[dx][dy] != 0 and (dx, dy) not in visited:
                    queue.append((dx, dy, distance + 1))
                    visited.add((dx, dy))
        
        return [[-x, -y] for _, _, x, y in sorted(heap, reverse = 1)]
        
        
        

class Solution {
    public List<List<Integer>> highestRankedKItems(
        int[][] grid, int[] pricing, int[] start, int k) {
        int m = grid.length, n = grid[0].length;
        int row = start[0], col = start[1];
        int low = pricing[0], high = pricing[1];
        List<int[]> items = new ArrayList<>();
        if (low <= grid[row][col] && grid[row][col] <= high) {
            items.add(new int[] {0, grid[row][col], row, col});
        }
        grid[row][col] = 0;
        Deque<int[]> q = new ArrayDeque<>();
        q.offer(new int[] {row, col, 0});
        int[] dirs = {-1, 0, 1, 0, -1};
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int i = p[0], j = p[1], d = p[2];
            for (int l = 0; l < 4; ++l) {
                int x = i + dirs[l], y = j + dirs[l + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] > 0) {
                    if (low <= grid[x][y] && grid[x][y] <= high) {
                        items.add(new int[] {d + 1, grid[x][y], x, y});
                    }
                    grid[x][y] = 0;
                    q.offer(new int[] {x, y, d + 1});
                }
            }
        }
        items.sort((a, b) -> {
            if (a[0] != b[0]) {
                return a[0] - b[0];
            }
            if (a[1] != b[1]) {
                return a[1] - b[1];
            }
            if (a[2] != b[2]) {
                return a[2] - b[2];
            }
            return a[3] - b[3];
        });
        List<List<Integer>> ans = new ArrayList<>();
        for (int i = 0; i < items.size() && i < k; ++i) {
            int[] p = items.get(i);
            ans.add(Arrays.asList(p[2], p[3]));
        }
        return ans;
    }
}

func highestRankedKItems(grid [][]int, pricing []int, start []int, k int) [][]int {
	m, n := len(grid), len(grid[0])
	row, col := start[0], start[1]
	low, high := pricing[0], pricing[1]
	var items [][]int
	if low <= grid[row][col] && grid[row][col] <= high {
		items = append(items, []int{0, grid[row][col], row, col})
	}
	q := [][]int{ {row, col, 0} }
	grid[row][col] = 0
	dirs := []int{-1, 0, 1, 0, -1}
	for len(q) > 0 {
		p := q[0]
		q = q[1:]
		i, j, d := p[0], p[1], p[2]
		for l := 0; l < 4; l++ {
			x, y := i+dirs[l], j+dirs[l+1]
			if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] > 0 {
				if low <= grid[x][y] && grid[x][y] <= high {
					items = append(items, []int{d + 1, grid[x][y], x, y})
				}
				grid[x][y] = 0
				q = append(q, []int{x, y, d + 1})
			}
		}
	}
	sort.Slice(items, func(i, j int) bool {
		a, b := items[i], items[j]
		if a[0] != b[0] {
			return a[0] < b[0]
		}
		if a[1] != b[1] {
			return a[1] < b[1]
		}
		if a[2] != b[2] {
			return a[2] < b[2]
		}
		return a[3] < b[3]
	})
	var ans [][]int
	for i := 0; i < len(items) && i < k; i++ {
		ans = append(ans, items[i][2:])
	}
	return ans
}

Solution 2. BFS + Heap

Instead of keeping all the reachable cells in ans, we can use a heap to keep only the optimal k cells.

Since we are doing BFS, we are already visiting the cells in ascending order of distance layer by layer, so we don’t need to sort by distance.

// OJ: https://leetcode.com/problems/k-highest-ranked-items-within-a-price-range/
// Time: O(MNlogK)
// Space: O(MN)
class Solution {
public:
    vector<vector<int>> highestRankedKItems(vector<vector<int>>& A, vector<int>& P, vector<int>& start, int k) {
        int M = A.size(), N = A[0].size(), step = 0, dirs[4][2] = { {0,1},{0,-1},{1,0},{-1,0} };
        queue<pair<int, int>> q{ { {start[0], start[1]} } };
        vector<vector<int>> ans;
        vector<vector<bool>> seen(M, vector<bool>(N));
        seen[start[0]][start[1]] = true;
        while (q.size() && ans.size() < k) {
            int cnt = q.size();
            vector<vector<int>> tmp;
            while (cnt--) {
                auto [x, y] = q.front();
                q.pop();
                if (A[x][y] >= P[0] && A[x][y] <= P[1]) tmp.push_back({A[x][y], x, y});
                for (auto &[dx, dy] : dirs) {
                    int a = x + dx, b = y + dy;
                    if (a < 0 || b < 0 || a >= M || b >= N || A[a][b] == 0 || seen[a][b]) continue;
                    seen[a][b] = true;
                    q.emplace(a, b);
                }
            }
            sort(begin(tmp), end(tmp));
            ++step;
            for (auto c : tmp) {
                ans.push_back({c[1], c[2]});
                if (ans.size() == k) break;
            }
        }
        return ans;
    }
};

class Solution:
    def highestRankedKItems(
        self, grid: List[List[int]], pricing: List[int], start: List[int], k: int
    ) -> List[List[int]]:
        m, n = len(grid), len(grid[0])
        row, col, low, high = start + pricing
        items = []
        if low <= grid[row][col] <= high:
            items.append([0, grid[row][col], row, col])
        q = deque([(row, col, 0)])
        grid[row][col] = 0
        while q:
            i, j, d = q.popleft()
            for a, b in [[0, 1], [0, -1], [1, 0], [-1, 0]]:
                x, y = i + a, j + b
                if 0 <= x < m and 0 <= y < n and grid[x][y]:
                    if low <= grid[x][y] <= high:
                        items.append([d + 1, grid[x][y], x, y])
                    q.append((x, y, d + 1))
                    grid[x][y] = 0
        items.sort()
        return [item[2:] for item in items][:k]

############

# 2146. K Highest Ranked Items Within a Price Range
# https://leetcode.com/problems/k-highest-ranked-items-within-a-price-range/

class Solution:
    def highestRankedKItems(self, grid: List[List[int]], pricing: List[int], start: List[int], k: int) -> List[List[int]]:
        rows, cols = len(grid), len(grid[0])
        heap = []
        sx, sy = start
        minP, maxP = pricing
        queue = deque([(sx, sy, 0)])
        visited = set([(sx, sy)])
        
        while queue:
            x, y, distance = queue.popleft()
            
            price = grid[x][y]

            if price != 1 and minP <= price <= maxP:
                if len(heap) == k:
                    heapq.heappushpop(heap, (-distance, -price, -x, -y))
                else:
                    heapq.heappush(heap, (-distance, -price, -x, -y))

            for dx, dy in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]:
                if 0 <= dx < rows and 0 <= dy < cols and grid[dx][dy] != 0 and (dx, dy) not in visited:
                    queue.append((dx, dy, distance + 1))
                    visited.add((dx, dy))
        
        return [[-x, -y] for _, _, x, y in sorted(heap, reverse = 1)]
        
        
        

class Solution {
    public List<List<Integer>> highestRankedKItems(
        int[][] grid, int[] pricing, int[] start, int k) {
        int m = grid.length, n = grid[0].length;
        int row = start[0], col = start[1];
        int low = pricing[0], high = pricing[1];
        List<int[]> items = new ArrayList<>();
        if (low <= grid[row][col] && grid[row][col] <= high) {
            items.add(new int[] {0, grid[row][col], row, col});
        }
        grid[row][col] = 0;
        Deque<int[]> q = new ArrayDeque<>();
        q.offer(new int[] {row, col, 0});
        int[] dirs = {-1, 0, 1, 0, -1};
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int i = p[0], j = p[1], d = p[2];
            for (int l = 0; l < 4; ++l) {
                int x = i + dirs[l], y = j + dirs[l + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] > 0) {
                    if (low <= grid[x][y] && grid[x][y] <= high) {
                        items.add(new int[] {d + 1, grid[x][y], x, y});
                    }
                    grid[x][y] = 0;
                    q.offer(new int[] {x, y, d + 1});
                }
            }
        }
        items.sort((a, b) -> {
            if (a[0] != b[0]) {
                return a[0] - b[0];
            }
            if (a[1] != b[1]) {
                return a[1] - b[1];
            }
            if (a[2] != b[2]) {
                return a[2] - b[2];
            }
            return a[3] - b[3];
        });
        List<List<Integer>> ans = new ArrayList<>();
        for (int i = 0; i < items.size() && i < k; ++i) {
            int[] p = items.get(i);
            ans.add(Arrays.asList(p[2], p[3]));
        }
        return ans;
    }
}

func highestRankedKItems(grid [][]int, pricing []int, start []int, k int) [][]int {
	m, n := len(grid), len(grid[0])
	row, col := start[0], start[1]
	low, high := pricing[0], pricing[1]
	var items [][]int
	if low <= grid[row][col] && grid[row][col] <= high {
		items = append(items, []int{0, grid[row][col], row, col})
	}
	q := [][]int{ {row, col, 0} }
	grid[row][col] = 0
	dirs := []int{-1, 0, 1, 0, -1}
	for len(q) > 0 {
		p := q[0]
		q = q[1:]
		i, j, d := p[0], p[1], p[2]
		for l := 0; l < 4; l++ {
			x, y := i+dirs[l], j+dirs[l+1]
			if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] > 0 {
				if low <= grid[x][y] && grid[x][y] <= high {
					items = append(items, []int{d + 1, grid[x][y], x, y})
				}
				grid[x][y] = 0
				q = append(q, []int{x, y, d + 1})
			}
		}
	}
	sort.Slice(items, func(i, j int) bool {
		a, b := items[i], items[j]
		if a[0] != b[0] {
			return a[0] < b[0]
		}
		if a[1] != b[1] {
			return a[1] < b[1]
		}
		if a[2] != b[2] {
			return a[2] < b[2]
		}
		return a[3] < b[3]
	})
	var ans [][]int
	for i := 0; i < len(items) && i < k; i++ {
		ans = append(ans, items[i][2:])
	}
	return ans
}

Discuss

https://leetcode.com/problems/k-highest-ranked-items-within-a-price-range/discuss/1709689/C%2B%2B-BFS-%2B-Sorting-O(MNlog(MN))-or-Heap-O(MNlogK)

2146 - K Highest Ranked Items Within a Price Range

2146. K Highest Ranked Items Within a Price Range (Medium)

Solution 1. BFS + Sorting

Solution 2. BFS + Heap

Discuss

All Problems

All Solutions

Welcome to Subscribe On Youtube

2146. K Highest Ranked Items Within a Price Range (Medium)

Solution 1. BFS + Sorting

Solution 2. BFS + Heap

Discuss

All Problems

All Solutions