Welcome to Subscribe On Youtube
2257. Count Unguarded Cells in the Grid
Description
You are given two integers m and n representing a 0-indexed m x n grid. You are also given two 2D integer arrays guards and walls where guards[i] = [rowi, coli] and walls[j] = [rowj, colj] represent the positions of the ith guard and jth wall respectively.
A guard can see every cell in the four cardinal directions (north, east, south, or west) starting from their position unless obstructed by a wall or another guard. A cell is guarded if there is at least one guard that can see it.
Return the number of unoccupied cells that are not guarded.
Example 1:
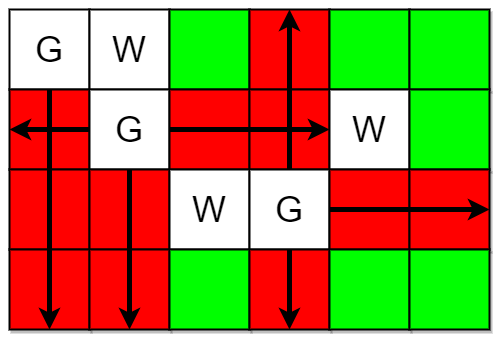
Input: m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]] Output: 7 Explanation: The guarded and unguarded cells are shown in red and green respectively in the above diagram. There are a total of 7 unguarded cells, so we return 7.
Example 2:
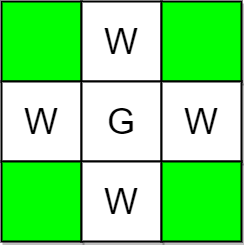
Input: m = 3, n = 3, guards = [[1,1]], walls = [[0,1],[1,0],[2,1],[1,2]] Output: 4 Explanation: The unguarded cells are shown in green in the above diagram. There are a total of 4 unguarded cells, so we return 4.
Constraints:
1 <= m, n <= 1052 <= m * n <= 1051 <= guards.length, walls.length <= 5 * 1042 <= guards.length + walls.length <= m * nguards[i].length == walls[j].length == 20 <= rowi, rowj < m0 <= coli, colj < n- All the positions in
guardsandwallsare unique.
Solutions
Solution 1: Simulation
We create a two-dimensional array $g$ of size $m \times n$, where $g[i][j]$ represents the cell in row $i$ and column $j$. Initially, the value of $g[i][j]$ is $0$, indicating that the cell is not guarded.
Then, we traverse all guards and walls, and set the value of $g[i][j]$ to $2$, indicating that these positions cannot be accessed.
Next, we traverse all guard positions, simulate in four directions from that position until we encounter a wall or guard, or go out of bounds. During the simulation, we set the value of the encountered cell to $1$, indicating that the cell is guarded.
Finally, we traverse $g$ and count the number of cells with a value of $0$, which is the answer.
The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$. Here, $m$ and $n$ are the number of rows and columns in the grid, respectively.
-
class Solution { public int countUnguarded(int m, int n, int[][] guards, int[][] walls) { int[][] g = new int[m][n]; for (var e : guards) { g[e[0]][e[1]] = 2; } for (var e : walls) { g[e[0]][e[1]] = 2; } int[] dirs = {-1, 0, 1, 0, -1}; for (var e : guards) { for (int k = 0; k < 4; ++k) { int x = e[0], y = e[1]; int a = dirs[k], b = dirs[k + 1]; while (x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && g[x + a][y + b] < 2) { x += a; y += b; g[x][y] = 1; } } } int ans = 0; for (var row : g) { for (int v : row) { if (v == 0) { ++ans; } } } return ans; } } -
class Solution { public: int countUnguarded(int m, int n, vector<vector<int>>& guards, vector<vector<int>>& walls) { int g[m][n]; memset(g, 0, sizeof(g)); for (auto& e : guards) { g[e[0]][e[1]] = 2; } for (auto& e : walls) { g[e[0]][e[1]] = 2; } int dirs[5] = {-1, 0, 1, 0, -1}; for (auto& e : guards) { for (int k = 0; k < 4; ++k) { int x = e[0], y = e[1]; int a = dirs[k], b = dirs[k + 1]; while (x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && g[x + a][y + b] < 2) { x += a; y += b; g[x][y] = 1; } } } int ans = 0; for (auto& row : g) { ans += count(row, row + n, 0); } return ans; } }; -
class Solution: def countUnguarded( self, m: int, n: int, guards: List[List[int]], walls: List[List[int]] ) -> int: g = [[0] * n for _ in range(m)] for i, j in guards: g[i][j] = 2 for i, j in walls: g[i][j] = 2 dirs = (-1, 0, 1, 0, -1) for i, j in guards: for a, b in pairwise(dirs): x, y = i, j while 0 <= x + a < m and 0 <= y + b < n and g[x + a][y + b] < 2: x, y = x + a, y + b g[x][y] = 1 return sum(v == 0 for row in g for v in row) -
func countUnguarded(m int, n int, guards [][]int, walls [][]int) (ans int) { g := make([][]int, m) for i := range g { g[i] = make([]int, n) } for _, e := range guards { g[e[0]][e[1]] = 2 } for _, e := range walls { g[e[0]][e[1]] = 2 } dirs := [5]int{-1, 0, 1, 0, -1} for _, e := range guards { for k := 0; k < 4; k++ { x, y := e[0], e[1] a, b := dirs[k], dirs[k+1] for x+a >= 0 && x+a < m && y+b >= 0 && y+b < n && g[x+a][y+b] < 2 { x, y = x+a, y+b g[x][y] = 1 } } } for _, row := range g { for _, v := range row { if v == 0 { ans++ } } } return } -
function countUnguarded(m: number, n: number, guards: number[][], walls: number[][]): number { const g: number[][] = Array.from({ length: m }, () => Array.from({ length: n }, () => 0)); for (const [i, j] of guards) { g[i][j] = 2; } for (const [i, j] of walls) { g[i][j] = 2; } const dirs: number[] = [-1, 0, 1, 0, -1]; for (const [i, j] of guards) { for (let k = 0; k < 4; ++k) { let [x, y] = [i, j]; let [a, b] = [dirs[k], dirs[k + 1]]; while (x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && g[x + a][y + b] < 2) { x += a; y += b; g[x][y] = 1; } } } let ans = 0; for (const row of g) { for (const v of row) { ans += v === 0 ? 1 : 0; } } return ans; } -
function countUnguarded(m, n, guards, walls) { const g = Array.from({ length: m }, () => Array.from({ length: n }, () => 0)); for (const [i, j] of guards) { g[i][j] = 2; } for (const [i, j] of walls) { g[i][j] = 2; } const dirs = [-1, 0, 1, 0, -1]; for (const [i, j] of guards) { for (let k = 0; k < 4; ++k) { let [x, y] = [i, j]; let [a, b] = [dirs[k], dirs[k + 1]]; while (x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && g[x + a][y + b] < 2) { x += a; y += b; g[x][y] = 1; } } } let ans = 0; for (const row of g) { for (const v of row) { ans += v === 0 ? 1 : 0; } } return ans; }