Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2141.html
2141. Maximum Running Time of N Computers
- Difficulty: Hard.
- Related Topics: Array, Binary Search, Greedy, Sorting.
- Similar Questions: Minimum Moves to Equal Array Elements, Sell Diminishing-Valued Colored Balls, Maximum Number of Tasks You Can Assign, Minimum Time to Complete Trips, Minimum Amount of Time to Fill Cups.
Problem
You have n computers. You are given the integer n and a 0-indexed integer array batteries where the ith battery can run a computer for batteries[i] minutes. You are interested in running all n computers simultaneously using the given batteries.
Initially, you can insert at most one battery into each computer. After that and at any integer time moment, you can remove a battery from a computer and insert another battery any number of times. The inserted battery can be a totally new battery or a battery from another computer. You may assume that the removing and inserting processes take no time.
Note that the batteries cannot be recharged.
Return the **maximum number of minutes you can run all the n computers simultaneously.**
Example 1:

Input: n = 2, batteries = [3,3,3]
Output: 4
Explanation:
Initially, insert battery 0 into the first computer and battery 1 into the second computer.
After two minutes, remove battery 1 from the second computer and insert battery 2 instead. Note that battery 1 can still run for one minute.
At the end of the third minute, battery 0 is drained, and you need to remove it from the first computer and insert battery 1 instead.
By the end of the fourth minute, battery 1 is also drained, and the first computer is no longer running.
We can run the two computers simultaneously for at most 4 minutes, so we return 4.
Example 2:
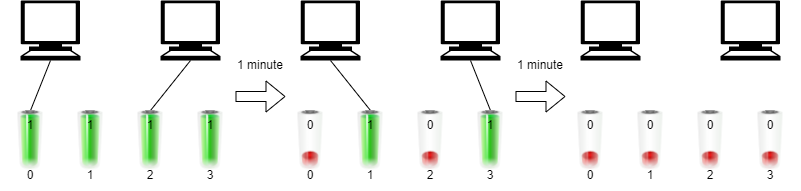
Input: n = 2, batteries = [1,1,1,1]
Output: 2
Explanation:
Initially, insert battery 0 into the first computer and battery 2 into the second computer.
After one minute, battery 0 and battery 2 are drained so you need to remove them and insert battery 1 into the first computer and battery 3 into the second computer.
After another minute, battery 1 and battery 3 are also drained so the first and second computers are no longer running.
We can run the two computers simultaneously for at most 2 minutes, so we return 2.
Constraints:
-
1 <= n <= batteries.length <= 105 -
1 <= batteries[i] <= 109
Solution
-
class Solution { private boolean isPossibeToRun(int n, int[] batteries, long avgTime) { long duration = 0; for (long ele : batteries) { duration += Math.min(ele, avgTime); } return avgTime * n <= duration; } public long maxRunTime(int n, int[] batteries) { long startTime = 0; long sum = 0; long ans = 0; for (long ele : batteries) { sum += ele; } long endTime = sum; while (startTime <= endTime) { long avgTime = (startTime + endTime) / 2; if (isPossibeToRun(n, batteries, avgTime)) { ans = avgTime; startTime = avgTime + 1; } else { endTime = avgTime - 1; } } return ans; } } -
# 2141. Maximum Running Time of N Computers # https://leetcode.com/problems/maximum-running-time-of-n-computers class Solution: def maxRunTime(self, n: int, batteries: List[int]) -> int: def good(k): target = n * k have = 0 for x in batteries: have += min(x, k) return have >= target total = sum(batteries) left, right = 0, total // n res = -1 while left <= right: mid = left + (right - left) // 2 if good(mid): res = mid left = mid + 1 else: right = mid - 1 return res -
impl Solution { #[allow(dead_code)] pub fn max_run_time(n: i32, batteries: Vec<i32>) -> i64 { // First sort the batteries let mut batteries = batteries; let m = batteries.len() as i32; batteries.sort(); let mut extra_sum: i64 = 0; for i in 0..(m - n) as usize { extra_sum += batteries[i] as i64; } let mut i = (m - n) as usize; let mut cur_height = batteries[i]; let mut ret = cur_height as i64; while extra_sum != 0 { if i + 1 == m as usize { assert!(cur_height == *batteries.last().unwrap()); ret += extra_sum / n as i64; break; } if batteries[i] == batteries[i + 1] { i += 1; continue; } let diff = extra_sum / (i - (m - n) as usize + 1) as i64; if (cur_height as i64 + diff) <= batteries[i + 1] as i64 { ret = cur_height as i64 + diff; break; } else { extra_sum -= (batteries[i + 1] - batteries[i]) as i64 * (i - (m - n) as usize + 1) as i64; ret = batteries[i + 1] as i64; } i += 1; if i != m as usize { cur_height = batteries[i]; } } ret } } -
class Solution { public: long long maxRunTime(int n, vector<int>& batteries) { long long l = 0, r = 0; for (int x : batteries) { r += x; } while (l < r) { long long mid = (l + r + 1) >> 1; long long s = 0; for (int x : batteries) { s += min(1LL * x, mid); } if (s >= n * mid) { l = mid; } else { r = mid - 1; } } return l; } }; -
func maxRunTime(n int, batteries []int) int64 { l, r := 0, 0 for _, x := range batteries { r += x } for l < r { mid := (l + r + 1) >> 1 s := 0 for _, x := range batteries { s += min(x, mid) } if s >= n*mid { l = mid } else { r = mid - 1 } } return int64(l) } func min(a, b int) int { if a < b { return a } return b } -
function maxRunTime(n: number, batteries: number[]): number { let l = 0n; let r = 0n; for (const x of batteries) { r += BigInt(x); } while (l < r) { const mid = (l + r + 1n) >> 1n; let s = 0n; for (const x of batteries) { s += BigInt(Math.min(x, Number(mid))); } if (s >= mid * BigInt(n)) { l = mid; } else { r = mid - 1n; } } return Number(l); }
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).