Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2132.html
2132. Stamping the Grid
- Difficulty: Hard.
- Related Topics: Array, Greedy, Matrix, Prefix Sum.
- Similar Questions: Maximal Square, Bomb Enemy, Matrix Block Sum.
Problem
You are given an m x n binary matrix grid where each cell is either 0 (empty) or 1 (occupied).
You are then given stamps of size stampHeight x stampWidth. We want to fit the stamps such that they follow the given restrictions and requirements:
-
Cover all the empty cells.
-
Do not cover any of the occupied cells.
-
We can put as many stamps as we want.
-
Stamps can overlap with each other.
-
Stamps are not allowed to be rotated.
-
Stamps must stay completely inside the grid.
Return true if it is possible to fit the stamps while following the given restrictions and requirements. Otherwise, return false.
Example 1:
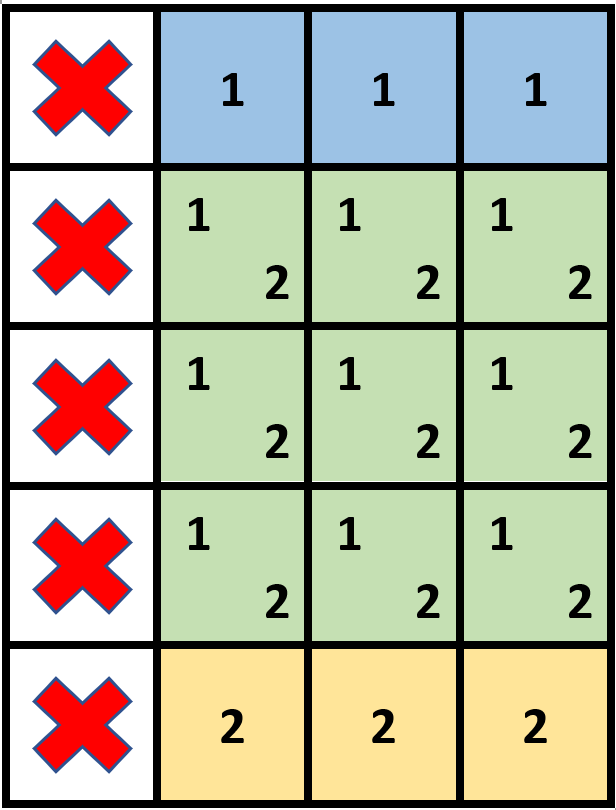
Input: grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3
Output: true
Explanation: We have two overlapping stamps (labeled 1 and 2 in the image) that are able to cover all the empty cells.
Example 2:
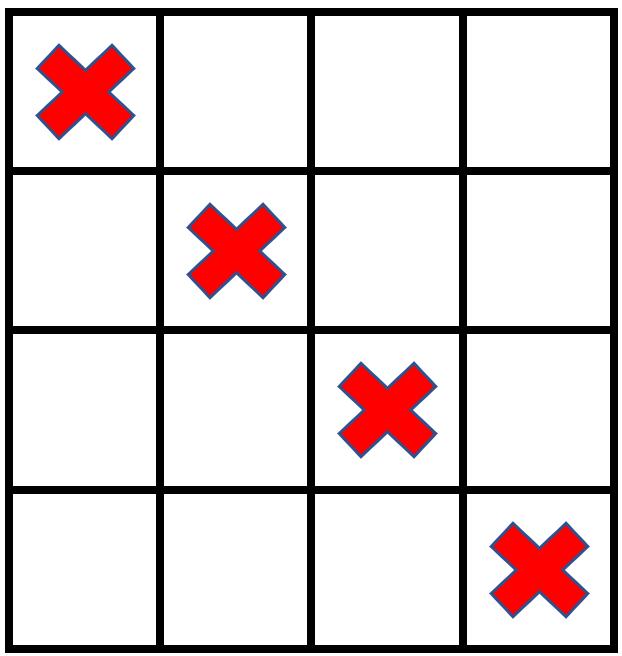
Input: grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2
Output: false
Explanation: There is no way to fit the stamps onto all the empty cells without the stamps going outside the grid.
Constraints:
-
m == grid.length -
n == grid[r].length -
1 <= m, n <= 105 -
1 <= m * n <= 2 * 105 -
grid[r][c]is either0or1. -
1 <= stampHeight, stampWidth <= 105
Solution
-
class Solution { private boolean canPaved(int[][] grid, int is, int js, int ie, int je) { for (int i = is; i <= ie; i++) { for (int j = js; j <= je; j++) { if (grid[i][j] == 1) { return true; } } } return false; } public boolean possibleToStamp(int[][] grid, int h, int w) { int rl = grid[0].length; for (int i = 0; i < grid.length; i++) { int[] row = grid[i]; int prev = -1; for (int j = 0; j < row.length; j++) { if (row[j] == 0) { if (j + 1 < rl && row[j + 1] == 1 && j - w + 1 >= 0 && i + 1 < grid.length && grid[i + 1][j] == 1 && i - h + 1 >= 0 && canPaved(grid, i - h + 1, j - w + 1, i, j)) { return false; } continue; } if (1 < j - prev && j - prev <= w) { return false; } prev = j; } if (1 < row.length - prev && row.length - prev <= w) { return false; } } for (int i = 0; i < rl; i++) { int prev = -1; for (int j = 0; j < grid.length; j++) { if (grid[j][i] == 0) { continue; } if (1 < j - prev && j - prev <= h) { return false; } prev = j; } if (1 < grid.length - prev && grid.length - prev <= h) { return false; } } return true; } } ############ class Solution { public boolean possibleToStamp(int[][] grid, int stampHeight, int stampWidth) { int m = grid.length, n = grid[0].length; int[][] s = new int[m + 1][n + 1]; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + grid[i][j]; } } int[][] d = new int[m + 1][n + 1]; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (grid[i][j] == 0) { int x = i + stampHeight, y = j + stampWidth; if (x <= m && y <= n && s[x][y] - s[x][j] - s[i][y] + s[i][j] == 0) { d[i][j]++; d[i][y]--; d[x][j]--; d[x][y]++; } } } } int[][] cnt = new int[m + 1][n + 1]; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { cnt[i + 1][j + 1] = cnt[i + 1][j] + cnt[i][j + 1] - cnt[i][j] + d[i][j]; if (grid[i][j] == 0 && cnt[i + 1][j + 1] == 0) { return false; } } } return true; } } -
class Solution: def possibleToStamp( self, grid: List[List[int]], stampHeight: int, stampWidth: int ) -> bool: m, n = len(grid), len(grid[0]) s = [[0] * (n + 1) for _ in range(m + 1)] for i, row in enumerate(grid): for j, v in enumerate(row): s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + v d = [[0] * (n + 1) for _ in range(m + 1)] for i, row in enumerate(grid): for j, v in enumerate(row): if v == 0: x, y = i + stampHeight, j + stampWidth if x <= m and y <= n and s[x][y] - s[x][j] - s[i][y] + s[i][j] == 0: d[i][j] += 1 d[i][y] -= 1 d[x][j] -= 1 d[x][y] += 1 cnt = [[0] * (n + 1) for _ in range(m + 1)] for i, row in enumerate(grid): for j, v in enumerate(row): cnt[i + 1][j + 1] = cnt[i + 1][j] + cnt[i][j + 1] - cnt[i][j] + d[i][j] if v == 0 and cnt[i + 1][j + 1] == 0: return False return True ############ # 2132. Stamping the Grid # https://leetcode.com/problems/stamping-the-grid/ class Solution: def possibleToStamp(self, grid: List[List[int]], H: int, W: int) -> bool: rows, cols = len(grid), len(grid[0]) prefix = [[0] * (cols + 1) for _ in range(rows + 1)] for x in range(rows): for y in range(cols): prefix[x + 1][y + 1] = prefix[x + 1][y] + prefix[x][y + 1] - prefix[x][y] + grid[x][y] diff = [[0] * (cols + 1) for _ in range(rows + 1)] for x in range(rows - H + 1): for y in range(cols - W + 1): rect = prefix[x + H][y + W] - prefix[x + H][y] - prefix[x][y + W] + prefix[x][y] if rect == 0: diff[x][y] += 1 diff[x + H][y] -= 1 diff[x][y + W] -= 1 diff[x + H][y + W] += 1 for x in range(rows + 1): for y in range(cols): diff[x][y + 1] += diff[x][y] for y in range(cols + 1): for x in range(rows): diff[x + 1][y] += diff[x][y] for x in range(rows): for y in range(cols): if grid[x][y] == 0 and diff[x][y] == 0: return False return True -
class Solution { public: bool possibleToStamp(vector<vector<int>>& grid, int stampHeight, int stampWidth) { int m = grid.size(), n = grid[0].size(); vector<vector<int>> s(m + 1, vector<int>(n + 1)); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + grid[i][j]; } } vector<vector<int>> d(m + 1, vector<int>(n + 1)); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (grid[i][j]) continue; int x = i + stampHeight, y = j + stampWidth; if (x <= m && y <= n && s[x][y] - s[i][y] - s[x][j] + s[i][j] == 0) { d[i][j]++; d[x][j]--; d[i][y]--; d[x][y]++; } } } vector<vector<int>> cnt(m + 1, vector<int>(n + 1)); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { cnt[i + 1][j + 1] = cnt[i + 1][j] + cnt[i][j + 1] - cnt[i][j] + d[i][j]; if (grid[i][j] == 0 && cnt[i + 1][j + 1] == 0) return false; } } return true; } }; -
func possibleToStamp(grid [][]int, stampHeight int, stampWidth int) bool { m, n := len(grid), len(grid[0]) s := make([][]int, m+1) d := make([][]int, m+1) cnt := make([][]int, m+1) for i := range s { s[i] = make([]int, n+1) d[i] = make([]int, n+1) cnt[i] = make([]int, n+1) } for i, row := range grid { for j, v := range row { s[i+1][j+1] = s[i+1][j] + s[i][j+1] - s[i][j] + v } } for i, row := range grid { for j, v := range row { if v == 0 { x, y := i+stampHeight, j+stampWidth if x <= m && y <= n && s[x][y]-s[i][y]-s[x][j]+s[i][j] == 0 { d[i][j]++ d[i][y]-- d[x][j]-- d[x][y]++ } } } } for i, row := range grid { for j, v := range row { cnt[i+1][j+1] = cnt[i+1][j] + cnt[i][j+1] - cnt[i][j] + d[i][j] if v == 0 && cnt[i+1][j+1] == 0 { return false } } } return true } -
/** * @param {number[][]} grid * @param {number} stampHeight * @param {number} stampWidth * @return {boolean} */ var possibleToStamp = function (grid, stampHeight, stampWidth) { const m = grid.length; const n = grid[0].length; let s = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0)); let d = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0)); let cnt = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0)); for (let i = 0; i < m; ++i) { for (let j = 0; j < n; ++j) { s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + grid[i][j]; } } for (let i = 0; i < m; ++i) { for (let j = 0; j < n; ++j) { if (grid[i][j] == 0) { let [x, y] = [i + stampHeight, j + stampWidth]; if ( x <= m && y <= n && s[x][y] - s[i][y] - s[x][j] + s[i][j] == 0 ) { d[i][j]++; d[i][y]--; d[x][j]--; d[x][y]++; } } } } for (let i = 0; i < m; ++i) { for (let j = 0; j < n; ++j) { cnt[i + 1][j + 1] = cnt[i + 1][j] + cnt[i][j + 1] - cnt[i][j] + d[i][j]; if (grid[i][j] == 0 && cnt[i + 1][j + 1] == 0) { return false; } } } return true; }; -
impl Solution { pub fn possible_to_stamp(grid: Vec<Vec<i32>>, stamp_height: i32, stamp_width: i32) -> bool { let n: usize = grid.len(); let m: usize = grid[0].len(); let mut prefix_vec: Vec<Vec<i32>> = vec![vec![0; m + 1]; n + 1]; // Initialize the prefix vector for i in 0..n { for j in 0..m { prefix_vec[i + 1][j + 1] = prefix_vec[i][j + 1] + prefix_vec[i + 1][j] - prefix_vec[i][j] + grid[i][j]; } } let mut diff_vec: Vec<Vec<i32>> = vec![vec![0; m + 1]; n + 1]; // Construct the difference vector based on prefix sum vector for i in 0..n { for j in 0..m { // If the value of the cell is one, just bypass this if grid[i][j] == 1 { continue; } // Otherwise, try stick the stamp let x: usize = i + stamp_height as usize; let y: usize = j + stamp_width as usize; // Check the bound if x <= n && y <= m { // If the region can be sticked (All cells are empty, which means the sum will be zero) if prefix_vec[x][y] - prefix_vec[x][j] - prefix_vec[i][y] + prefix_vec[i][j] == 0 { // Update the difference vector diff_vec[i][j] += 1; diff_vec[x][y] += 1; diff_vec[x][j] -= 1; diff_vec[i][y] -= 1; } } } } let mut check_vec: Vec<Vec<i32>> = vec![vec![0; m + 1]; n + 1]; // Check the prefix sum of difference vector, to determine if there is any empty cell left for i in 0..n { for j in 0..m { // If the value of the cell is one, just bypass this if grid[i][j] == 1 { continue; } // Otherwise, check if the region is empty, by calculating the prefix sum of difference vector check_vec[i + 1][j + 1] = check_vec[i][j + 1] + check_vec[i + 1][j] - check_vec[i][j] + diff_vec[i][j]; if check_vec[i + 1][j + 1] == 0 { return false; } } } true } } -
function possibleToStamp(grid: number[][], stampHeight: number, stampWidth: number): boolean { const m = grid.length; const n = grid[0].length; const s: number[][] = Array.from({ length: m + 1 }, () => Array(n + 1).fill(0)); for (let i = 1; i <= m; ++i) { for (let j = 1; j <= n; ++j) { s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + grid[i - 1][j - 1]; } } const d: number[][] = Array.from({ length: m + 2 }, () => Array(n + 2).fill(0)); for (let i = 1; i + stampHeight - 1 <= m; ++i) { for (let j = 1; j + stampWidth - 1 <= n; ++j) { const [x, y] = [i + stampHeight - 1, j + stampWidth - 1]; if (s[x][y] - s[x][j - 1] - s[i - 1][y] + s[i - 1][j - 1] === 0) { d[i][j]++; d[i][y + 1]--; d[x + 1][j]--; d[x + 1][y + 1]++; } } } for (let i = 1; i <= m; ++i) { for (let j = 1; j <= n; ++j) { d[i][j] += d[i - 1][j] + d[i][j - 1] - d[i - 1][j - 1]; if (grid[i - 1][j - 1] === 0 && d[i][j] === 0) { return false; } } } return true; }
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).