Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2101.html
2101. Detonate the Maximum Bombs (Medium)
You are given a list of bombs. The range of a bomb is defined as the area where its effect can be felt. This area is in the shape of a circle with the center as the location of the bomb.
The bombs are represented by a 0-indexed 2D integer array bombs where bombs[i] = [xi, yi, ri]. xi and yi denote the X-coordinate and Y-coordinate of the location of the ith bomb, whereas ri denotes the radius of its range.
You may choose to detonate a single bomb. When a bomb is detonated, it will detonate all bombs that lie in its range. These bombs will further detonate the bombs that lie in their ranges.
Given the list of bombs, return the maximum number of bombs that can be detonated if you are allowed to detonate only one bomb.
Example 1:
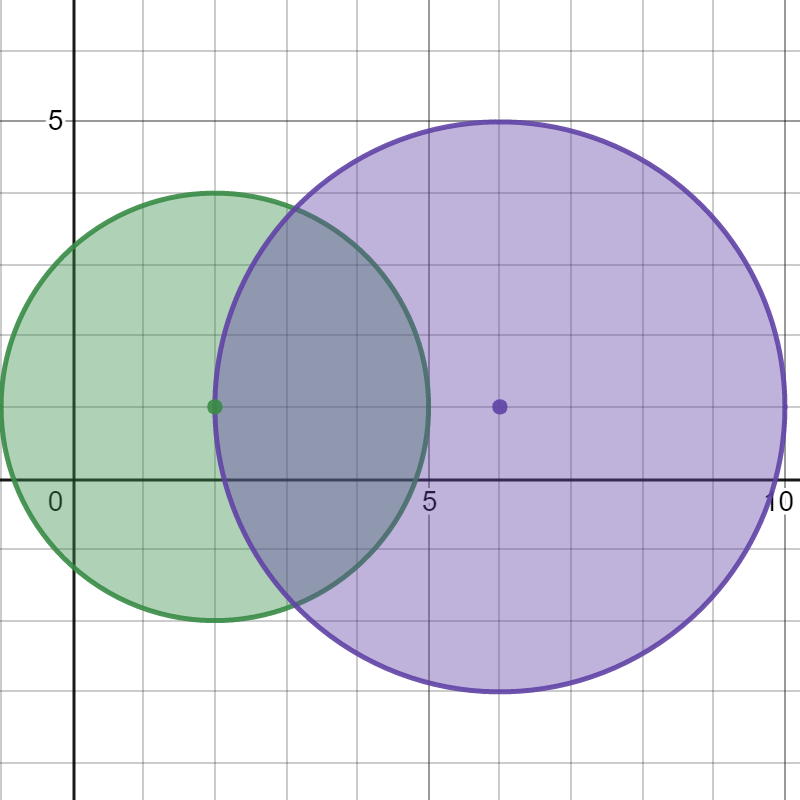
Input: bombs = [[2,1,3],[6,1,4]] Output: 2 Explanation: The above figure shows the positions and ranges of the 2 bombs. If we detonate the left bomb, the right bomb will not be affected. But if we detonate the right bomb, both bombs will be detonated. So the maximum bombs that can be detonated is max(1, 2) = 2.
Example 2:
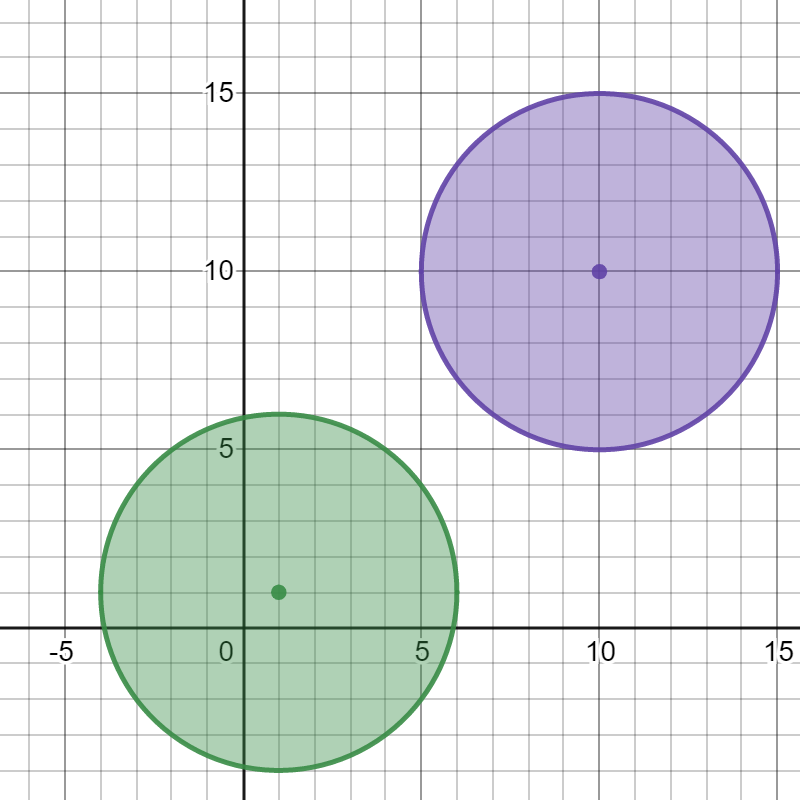
Input: bombs = [[1,1,5],[10,10,5]] Output: 1 Explanation: Detonating either bomb will not detonate the other bomb, so the maximum number of bombs that can be detonated is 1.
Example 3:
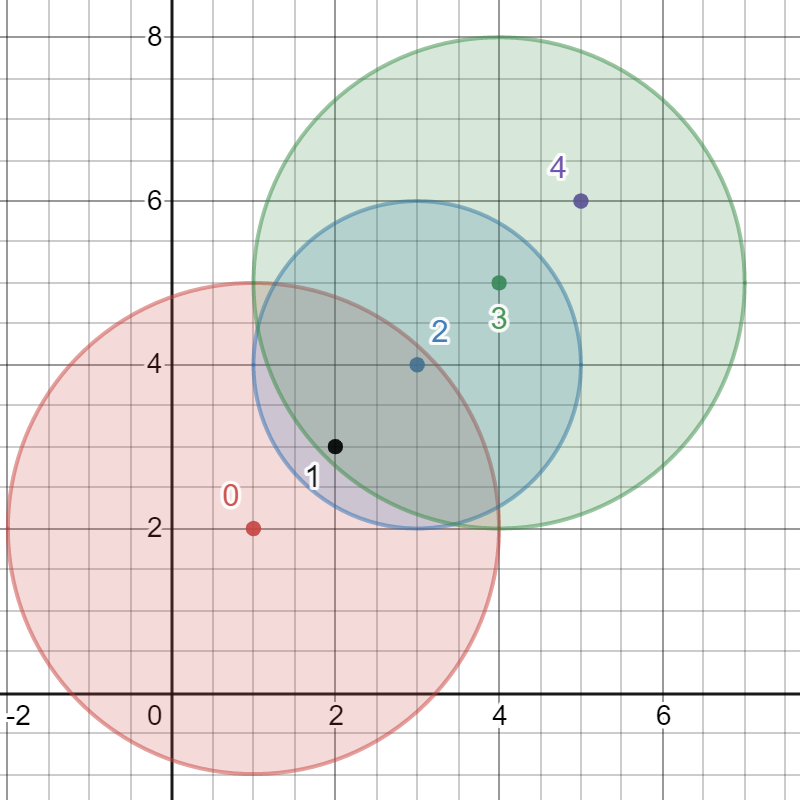
Input: bombs = [[1,2,3],[2,3,1],[3,4,2],[4,5,3],[5,6,4]] Output: 5 Explanation: The best bomb to detonate is bomb 0 because: - Bomb 0 detonates bombs 1 and 2. The red circle denotes the range of bomb 0. - Bomb 2 detonates bomb 3. The blue circle denotes the range of bomb 2. - Bomb 3 detonates bomb 4. The green circle denotes the range of bomb 3. Thus all 5 bombs are detonated.
Constraints:
1 <= bombs.length <= 100bombs[i].length == 31 <= xi, yi, ri <= 105
Similar Questions:
- Minesweeper (Medium)
- Number of Provinces (Medium)
- Max Area of Island (Medium)
- Rotting Oranges (Medium)
Solution 1. DFS
Time complexity: In the worst case, all N nodes are inter-connected. So for each node we need to enumerate its N neighbors. So the DFS has O(N^2) time complexity, and we need to repeat the DFS N times. Thus the overall time complexity is O(N^3).
// OJ: https://leetcode.com/problems/detonate-the-maximum-bombs/
// Time: O(N^3)
// Space: O(N^2)
class Solution {
public:
int maximumDetonation(vector<vector<int>>& A) {
int N = A.size();
vector<vector<int>> G(N);
auto cover = [&](int i, int j) {
return pow((long)A[i][0] - A[j][0], 2) + pow((long)A[i][1] - A[j][1], 2) <= pow((long)A[i][2], 2);
};
for (int i = 0; i < N; ++i) {
for (int j = i + 1; j < N; ++j) {
if (cover(i, j)) G[i].push_back(j);
if (cover(j, i)) G[j].push_back(i);
}
}
vector<bool> seen(N);
function<int(int)> dfs = [&](int u) {
seen[u] = true;
int ans = 1;
for (int v : G[u]) {
if (seen[v]) continue;
ans += dfs(v);
}
return ans;
};
int ans = 0;
for (int i = 0; i < N; ++i) {
seen.assign(N, false);
ans = max(ans, dfs(i));
}
return ans;
}
};