Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2093.html
2093. Minimum Cost to Reach City With Discounts (Medium)
A series of highways connect n cities numbered from 0 to n - 1. You are given a 2D integer array highways where highways[i] = [city1i, city2i, tolli] indicates that there is a highway that connects city1i and city2i, allowing a car to go from city1i to city2i and vice versa for a cost of tolli.
You are also given an integer discounts which represents the number of discounts you have. You can use a discount to travel across the ith highway for a cost of tolli / 2 (integer division). Each discount may only be used once, and you can only use at most one discount per highway.
Return the minimum total cost to go from city 0 to city n - 1, or -1 if it is not possible to go from city 0 to city n - 1.
Example 1:
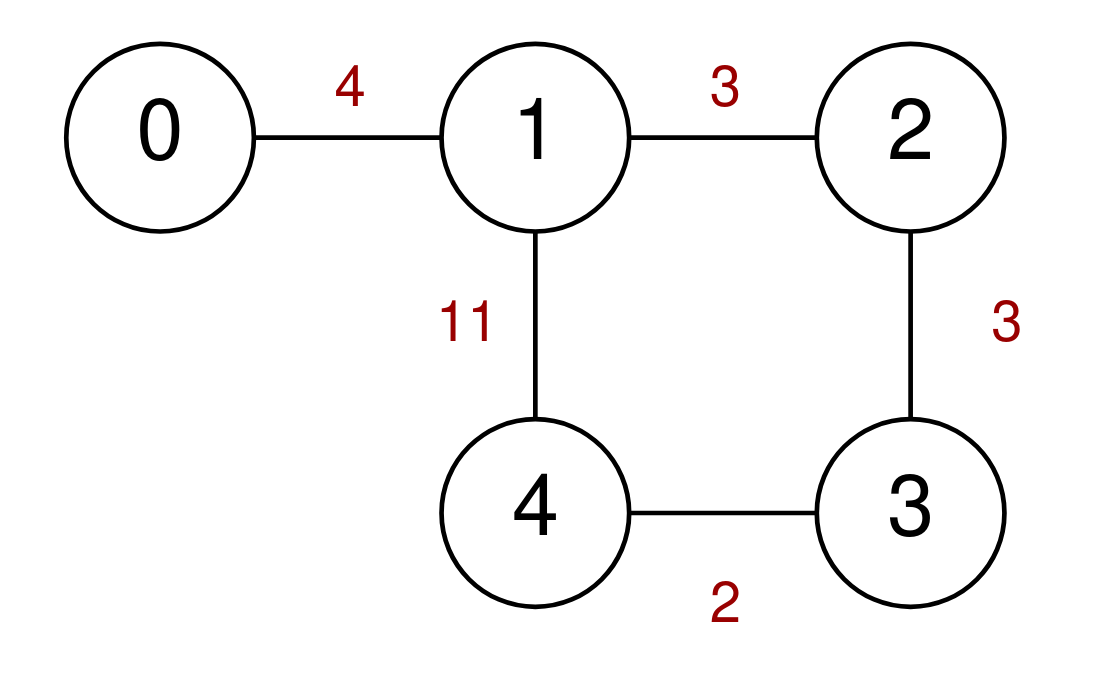
Input: n = 5, highways = [[0,1,4],[2,1,3],[1,4,11],[3,2,3],[3,4,2]], discounts = 1 Output: 9 Explanation: Go from 0 to 1 for a cost of 4. Go from 1 to 4 and use a discount for a cost of 11 / 2 = 5. The minimum cost to go from 0 to 4 is 4 + 5 = 9.
Example 2:
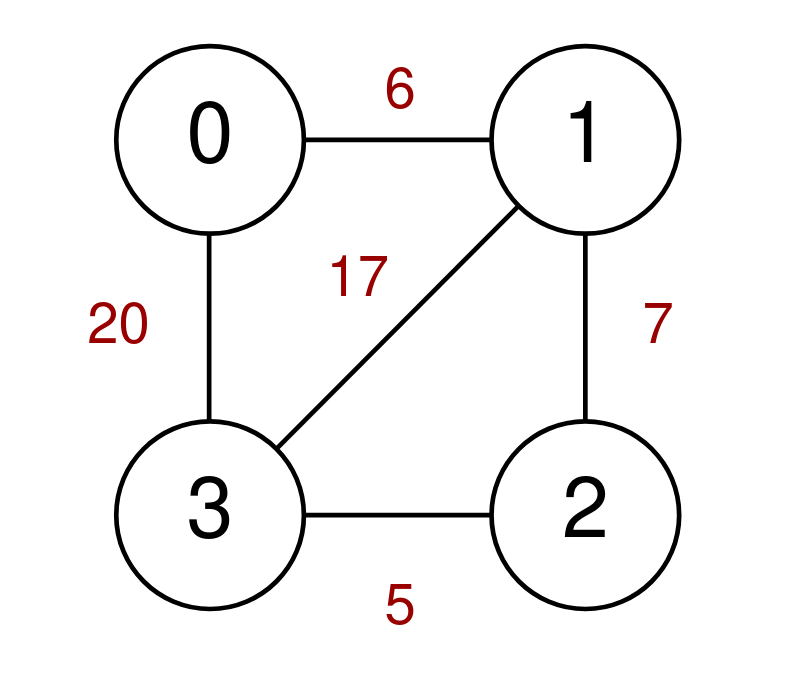
Input: n = 4, highways = [[1,3,17],[1,2,7],[3,2,5],[0,1,6],[3,0,20]], discounts = 20 Output: 8 Explanation: Go from 0 to 1 and use a discount for a cost of 6 / 2 = 3. Go from 1 to 2 and use a discount for a cost of 7 / 2 = 3. Go from 2 to 3 and use a discount for a cost of 5 / 2 = 2. The minimum cost to go from 0 to 3 is 3 + 3 + 2 = 8.
Example 3:
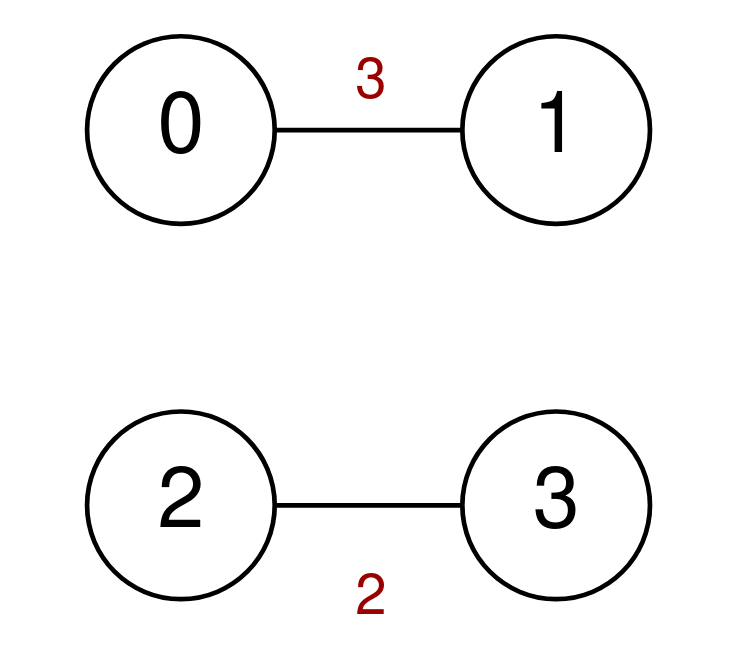
Input: n = 4, highways = [[0,1,3],[2,3,2]], discounts = 0 Output: -1 Explanation: It is impossible to go from 0 to 3 so return -1.
Constraints:
2 <= n <= 10001 <= highways.length <= 1000highways[i].length == 30 <= city1i, city2i <= n - 1city1i != city2i0 <= tolli <= 1050 <= discounts <= 500- There are no duplicate highways.
Companies:
Flipkart
Related Topics:
Graph, Shortest Path
Similar Questions:
- Cheapest Flights Within K Stops (Medium)
- Connecting Cities With Minimum Cost (Medium)
- Minimum Cost to Reach Destination in Time (Hard)
Solution 1. Dijkstra
dist[i][j] is the minimum cost going from node 0 to node j with i discounts. The answer is dist[d][N - 1].
We can use Dijkstra algorithm layer by layer from 0 discounts to d discounts.
When we extending from node u to node v, we have two options:
- Don’t the discount on the edge
u -> v. The new cost isdist[i][u] + weight[u][v] - Use the discount on the edge
u -> v. The new cost isdist[i-1][u] + weight[u][v] / 2.
We pick the smaller one out of them, say newCost, and update dist[i][v] if newCost < dist[i][v].
// OJ: https://leetcode.com/problems/minimum-cost-to-reach-city-with-discounts/
// Time: O(DElogE)
// Space: O(DN + E)
class Solution {
public:
int minimumCost(int n, vector<vector<int>>& E, int d) {
vector<unordered_map<int, int>> G(n);
for (auto &e : E) {
int u = e[0], v = e[1], w = e[2];
G[u][v] = w;
G[v][u] = w;
}
vector<vector<int>> dist(d + 1, vector<int>(n, INT_MAX));
auto dijkstra = [&](int i) {
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
pq.emplace(0, 0);
dist[i][0] = 0;
while (pq.size()) {
auto [cost, u] = pq.top();
pq.pop();
if (cost > dist[i][u]) continue;
for (auto &[v, w] : G[u]) {
int keep = cost + w, use = i > 0 ? dist[i - 1][u] + w / 2 : INT_MAX, newCost = min(use, keep);
if (dist[i][v] > newCost) {
dist[i][v] = newCost;
pq.emplace(dist[i][v], v);
}
}
}
};
for (int i = 0; i <= d; ++i) dijkstra(i);
return dist[d][n - 1] == INT_MAX ? -1 : dist[d][n - 1];
}
};
Solution 2. Dijkstra
// OJ: https://leetcode.com/problems/minimum-cost-to-reach-city-with-discounts/
// Time: O(DElogE)
// Space: O(DN + E)
class Solution {
typedef array<int, 3> item; // distance, cityId, # of discount left
public:
int minimumCost(int n, vector<vector<int>>& E, int discounts) {
vector<unordered_map<int, int>> G(n);
for (auto &e : E) {
int u = e[0], v = e[1], w = e[2];
G[u][v] = w;
G[v][u] = w;
}
vector<vector<int>> dist(discounts + 1, vector<int>(n, INT_MAX));
priority_queue<item, vector<item>, greater<>> pq;
pq.push({0, 0, discounts});
for (int i = 0; i <= discounts; ++i) dist[i][0] = 0;
while (pq.size()) {
auto [cost, u, d] = pq.top();
pq.pop();
if (cost > dist[d][u]) continue;
if (u == n - 1) return cost;
for (auto &[v, w] : G[u]) {
if (dist[d][v] > cost + w) {
dist[d][v] = cost + w;
pq.push({ dist[d][v], v, d });
}
if (d > 0 && dist[d - 1][v] > cost + w / 2) {
dist[d - 1][v] = cost + w / 2;
pq.push({ dist[d - 1][v], v, d - 1 });
}
}
}
return -1;
}
};