Welcome to Subscribe On Youtube

Formatted question description: https://leetcode.ca/all/2087.html

2087. Minimum Cost Homecoming of a Robot in a Grid (Medium)

There is an m x n grid, where (0, 0) is the top-left cell and (m - 1, n - 1) is the bottom-right cell. You are given an integer array startPos where startPos = [startrow, startcol] indicates that initially, a robot is at the cell (startrow, startcol). You are also given an integer array homePos where homePos = [homerow, homecol] indicates that its home is at the cell (homerow, homecol).

The robot needs to go to its home. It can move one cell in four directions: left, right, up, or down, and it can not move outside the boundary. Every move incurs some cost. You are further given two 0-indexed integer arrays: rowCosts of length m and colCosts of length n.

  • If the robot moves up or down into a cell whose row is r, then this move costs rowCosts[r].
  • If the robot moves left or right into a cell whose column is c, then this move costs colCosts[c].

Return the minimum total cost for this robot to return home.

 

Example 1:

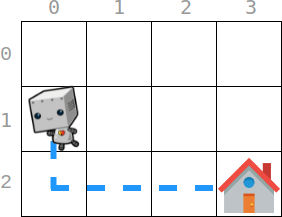
Input: startPos = [1, 0], homePos = [2, 3], rowCosts = [5, 4, 3], colCosts = [8, 2, 6, 7]
Output: 18
Explanation: One optimal path is that:
Starting from (1, 0)
-> It goes down to (2, 0). This move costs rowCosts[2] = 3.
-> It goes right to (2, 1). This move costs colCosts[1] = 2.
-> It goes right to (2, 2). This move costs colCosts[2] = 6.
-> It goes right to (2, 3). This move costs colCosts[3] = 7.
The total cost is 3 + 2 + 6 + 7 = 18

Example 2:

Input: startPos = [0, 0], homePos = [0, 0], rowCosts = [5], colCosts = [26]
Output: 0
Explanation: The robot is already at its home. Since no moves occur, the total cost is 0.

 

Constraints:

  • m == rowCosts.length
  • n == colCosts.length
  • 1 <= m, n <= 105
  • 0 <= rowCosts[r], colCosts[c] <= 104
  • startPos.length == 2
  • homePos.length == 2
  • 0 <= startrow, homerow < m
  • 0 <= startcol, homecol < n

Similar Questions:

Solution 1.

  • class Solution {
    public int minCost(int[] startPos, int[] homePos, int[] rowCosts, int[] colCosts) {
        int i = startPos[0], j = startPos[1];
        int x = homePos[0], y = homePos[1];
        int ans = 0;
        if (i < x) {
            for (int k = i + 1; k <= x; ++k) {
                ans += rowCosts[k];
            }
        } else {
            for (int k = x; k < i; ++k) {
                ans += rowCosts[k];
            }
        }
        if (j < y) {
            for (int k = j + 1; k <= y; ++k) {
                ans += colCosts[k];
            }
        } else {
            for (int k = y; k < j; ++k) {
                ans += colCosts[k];
            }
        }
        return ans;
    }
}

  • class Solution {
public:
    int minCost(vector<int>& startPos, vector<int>& homePos, vector<int>& rowCosts, vector<int>& colCosts) {
        int i = startPos[0], j = startPos[1];
        int x = homePos[0], y = homePos[1];
        int ans = 0;
        if (i < x) {
            ans += accumulate(rowCosts.begin() + i + 1, rowCosts.begin() + x + 1, 0);
        } else {
            ans += accumulate(rowCosts.begin() + x, rowCosts.begin() + i, 0);
        }
        if (j < y) {
            ans += accumulate(colCosts.begin() + j + 1, colCosts.begin() + y + 1, 0);
        } else {
            ans += accumulate(colCosts.begin() + y, colCosts.begin() + j, 0);
        }
        return ans;
    }
};

  • class Solution:
    def minCost(
        self,
        startPos: List[int],
        homePos: List[int],
        rowCosts: List[int],
        colCosts: List[int],
    ) -> int:
        i, j = startPos
        x, y = homePos
        ans = 0
        if i < x:
            ans += sum(rowCosts[i + 1 : x + 1])
        else:
            ans += sum(rowCosts[x:i])
        if j < y:
            ans += sum(colCosts[j + 1 : y + 1])
        else:
            ans += sum(colCosts[y:j])
        return ans


  • func minCost(startPos []int, homePos []int, rowCosts []int, colCosts []int) (ans int) {
	i, j := startPos[0], startPos[1]
	x, y := homePos[0], homePos[1]
	if i < x {
		ans += sum(rowCosts, i+1, x+1)
	} else {
		ans += sum(rowCosts, x, i)
	}
	if j < y {
		ans += sum(colCosts, j+1, y+1)
	} else {
		ans += sum(colCosts, y, j)
	}
	return
}

func sum(nums []int, i, j int) (s int) {
	for k := i; k < j; k++ {
		s += nums[k]
	}
	return
}

All Problems

All Solutions