Welcome to Subscribe On Youtube
2192. All Ancestors of a Node in a Directed Acyclic Graph
Description
You are given a positive integer n representing the number of nodes of a Directed Acyclic Graph (DAG). The nodes are numbered from 0 to n - 1 (inclusive).
You are also given a 2D integer array edges, where edges[i] = [fromi, toi] denotes that there is a unidirectional edge from fromi to toi in the graph.
Return a list answer, where answer[i] is the list of ancestors of the ith node, sorted in ascending order.
A node u is an ancestor of another node v if u can reach v via a set of edges.
Example 1:
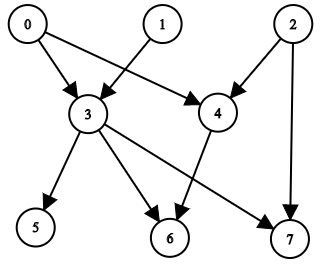
Input: n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]] Output: [[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]] Explanation: The above diagram represents the input graph. - Nodes 0, 1, and 2 do not have any ancestors. - Node 3 has two ancestors 0 and 1. - Node 4 has two ancestors 0 and 2. - Node 5 has three ancestors 0, 1, and 3. - Node 6 has five ancestors 0, 1, 2, 3, and 4. - Node 7 has four ancestors 0, 1, 2, and 3.
Example 2:
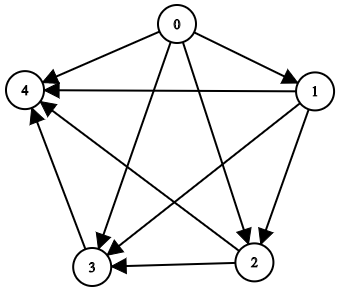
Input: n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]] Output: [[],[0],[0,1],[0,1,2],[0,1,2,3]] Explanation: The above diagram represents the input graph. - Node 0 does not have any ancestor. - Node 1 has one ancestor 0. - Node 2 has two ancestors 0 and 1. - Node 3 has three ancestors 0, 1, and 2. - Node 4 has four ancestors 0, 1, 2, and 3.
Constraints:
1 <= n <= 10000 <= edges.length <= min(2000, n * (n - 1) / 2)edges[i].length == 20 <= fromi, toi <= n - 1fromi != toi- There are no duplicate edges.
- The graph is directed and acyclic.
Solutions
BFS.
-
class Solution { private int n; private List<Integer>[] g; private List<List<Integer>> ans; public List<List<Integer>> getAncestors(int n, int[][] edges) { g = new List[n]; this.n = n; Arrays.setAll(g, i -> new ArrayList<>()); for (var e : edges) { g[e[0]].add(e[1]); } ans = new ArrayList<>(); for (int i = 0; i < n; ++i) { ans.add(new ArrayList<>()); } for (int i = 0; i < n; ++i) { bfs(i); } return ans; } private void bfs(int s) { Deque<Integer> q = new ArrayDeque<>(); q.offer(s); boolean[] vis = new boolean[n]; vis[s] = true; while (!q.isEmpty()) { int i = q.poll(); for (int j : g[i]) { if (!vis[j]) { vis[j] = true; q.offer(j); ans.get(j).add(s); } } } } } -
class Solution { public: vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) { vector<int> g[n]; for (auto& e : edges) { g[e[0]].push_back(e[1]); } vector<vector<int>> ans(n); auto bfs = [&](int s) { queue<int> q; q.push(s); bool vis[n]; memset(vis, 0, sizeof(vis)); vis[s] = true; while (q.size()) { int i = q.front(); q.pop(); for (int j : g[i]) { if (!vis[j]) { vis[j] = true; ans[j].push_back(s); q.push(j); } } } }; for (int i = 0; i < n; ++i) { bfs(i); } return ans; } }; -
class Solution: def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]: def bfs(s: int): q = deque([s]) vis = {s} while q: i = q.popleft() for j in g[i]: if j not in vis: vis.add(j) q.append(j) ans[j].append(s) g = defaultdict(list) for u, v in edges: g[u].append(v) ans = [[] for _ in range(n)] for i in range(n): bfs(i) return ans -
func getAncestors(n int, edges [][]int) [][]int { g := make([][]int, n) for _, e := range edges { g[e[0]] = append(g[e[0]], e[1]) } ans := make([][]int, n) bfs := func(s int) { q := []int{s} vis := make([]bool, n) vis[s] = true for len(q) > 0 { i := q[0] q = q[1:] for _, j := range g[i] { if !vis[j] { vis[j] = true q = append(q, j) ans[j] = append(ans[j], s) } } } } for i := 0; i < n; i++ { bfs(i) } return ans } -
function getAncestors(n: number, edges: number[][]): number[][] { const g: number[][] = Array.from({ length: n }, () => []); for (const [u, v] of edges) { g[u].push(v); } const ans: number[][] = Array.from({ length: n }, () => []); const bfs = (s: number) => { const q: number[] = [s]; const vis: boolean[] = Array.from({ length: n }, () => false); vis[s] = true; while (q.length) { const i = q.shift()!; for (const j of g[i]) { if (!vis[j]) { vis[j] = true; ans[j].push(s); q.push(j); } } } }; for (let i = 0; i < n; ++i) { bfs(i); } return ans; } -
public class Solution { private int n; private List<int>[] g; private IList<IList<int>> ans; public IList<IList<int>> GetAncestors(int n, int[][] edges) { g = new List<int>[n]; this.n = n; for (int i = 0; i < n; i++) { g[i] = new List<int>(); } foreach (var e in edges) { g[e[0]].Add(e[1]); } ans = new List<IList<int>>(); for (int i = 0; i < n; ++i) { ans.Add(new List<int>()); } for (int i = 0; i < n; ++i) { BFS(i); } return ans; } private void BFS(int s) { Queue<int> q = new Queue<int>(); q.Enqueue(s); bool[] vis = new bool[n]; vis[s] = true; while (q.Count > 0) { int i = q.Dequeue(); foreach (int j in g[i]) { if (!vis[j]) { vis[j] = true; q.Enqueue(j); ans[j].Add(s); } } } } }