Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2065.html
2065. Maximum Path Quality of a Graph (Hard)
There is an undirected graph with n nodes numbered from 0 to n - 1 (inclusive). You are given a 0-indexed integer array values where values[i] is the value of the ith node. You are also given a 0-indexed 2D integer array edges, where each edges[j] = [uj, vj, timej] indicates that there is an undirected edge between the nodes uj and vj, and it takes timej seconds to travel between the two nodes. Finally, you are given an integer maxTime.
A valid path in the graph is any path that starts at node 0, ends at node 0, and takes at most maxTime seconds to complete. You may visit the same node multiple times. The quality of a valid path is the sum of the values of the unique nodes visited in the path (each node's value is added at most once to the sum).
Return the maximum quality of a valid path.
Note: There are at most four edges connected to each node.
Example 1:
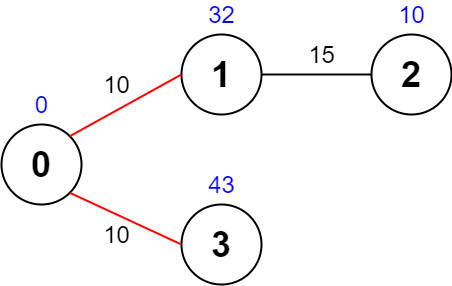
Input: values = [0,32,10,43], edges = [[0,1,10],[1,2,15],[0,3,10]], maxTime = 49 Output: 75 Explanation: One possible path is 0 -> 1 -> 0 -> 3 -> 0. The total time taken is 10 + 10 + 10 + 10 = 40 <= 49. The nodes visited are 0, 1, and 3, giving a maximal path quality of 0 + 32 + 43 = 75.
Example 2:
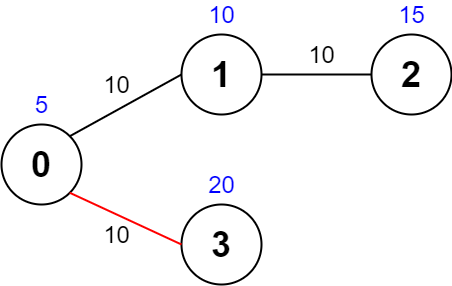
Input: values = [5,10,15,20], edges = [[0,1,10],[1,2,10],[0,3,10]], maxTime = 30 Output: 25 Explanation: One possible path is 0 -> 3 -> 0. The total time taken is 10 + 10 = 20 <= 30. The nodes visited are 0 and 3, giving a maximal path quality of 5 + 20 = 25.
Example 3:
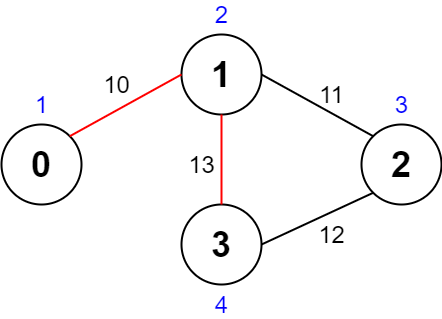
Input: values = [1,2,3,4], edges = [[0,1,10],[1,2,11],[2,3,12],[1,3,13]], maxTime = 50 Output: 7 Explanation: One possible path is 0 -> 1 -> 3 -> 1 -> 0. The total time taken is 10 + 13 + 13 + 10 = 46 <= 50. The nodes visited are 0, 1, and 3, giving a maximal path quality of 1 + 2 + 4 = 7.
Example 4:
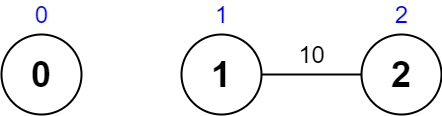
Input: values = [0,1,2], edges = [[1,2,10]], maxTime = 10 Output: 0 Explanation: The only path is 0. The total time taken is 0. The only node visited is 0, giving a maximal path quality of 0.
Constraints:
n == values.length1 <= n <= 10000 <= values[i] <= 1080 <= edges.length <= 2000edges[j].length == 30 <= uj < vj <= n - 110 <= timej, maxTime <= 100- All the pairs
[uj, vj]are unique. - There are at most four edges connected to each node.
- The graph may not be connected.
Similar Questions:
Solution 1. DFS
Since 10 <= timej, maxTime <= 100, the path at most have 10 edges. Since each node at most has 4 edges, the maximum number of possible paths is 4^10 ~= 1e6, so a brute force DFS should work.
// OJ: https://leetcode.com/problems/maximum-path-quality-of-a-graph/
// Time: O(4^10)
// Space: O(V + E)
class Solution {
public:
int maximalPathQuality(vector<int>& V, vector<vector<int>>& E, int maxTime) {
int N = V.size();
vector<vector<pair<int, int>>> G(N); // build graph
for (auto &e : E) {
int u = e[0], v = e[1], c = e[2];
G[u].emplace_back(v, c);
G[v].emplace_back(u, c);
}
vector<int> cnt(N); // `cnt[u]` is the number of times we've visted node `u` in the current path
int ans = 0;
function<void(int, int, int)> dfs = [&](int u, int val, int time) {
if (cnt[u] == 0) val += V[u];
cnt[u]++;
if (u == 0) ans = max(ans, val); // Only update answer if the current node is `0`.
for (auto &[v, c] : G[u]) {
if (time + c > maxTime) continue; // if the current time + the edge time is greater than maxTime, skip
dfs(v, val, time + c);
}
cnt[u]--;
};
dfs(0, 0, 0);
return ans;
}
};
Or we can optionally add Dijkstra to backtrack earlier.
// OJ: https://leetcode.com/problems/maximum-path-quality-of-a-graph/
// Time: O(ElogE + 4^10)
// Space: O(V + E)
class Solution {
typedef array<int, 2> T;
public:
int maximalPathQuality(vector<int>& V, vector<vector<int>>& E, int maxTime) {
int N = V.size();
vector<vector<array<int, 2>>> G(N); // build graph
for (auto &e : E) {
int u = e[0], v = e[1], c = e[2];
G[u].push_back({v, c});
G[v].push_back({u, c});
}
priority_queue<T, vector<T>, greater<T>> pq; // use Dijkstra to find the shortest distance from node 0 to all other nodes.
vector<int> dist(N, INT_MAX);
dist[0] = 0;
pq.push({0, 0});
while (pq.size()) {
auto [d, u] = pq.top();
pq.pop();
if (d > dist[u]) continue;
for (auto &[v, c] : G[u]) {
if (dist[v] > dist[u] + c) {
dist[v] = dist[u] + c;
pq.push({dist[v], v});
}
}
}
vector<int> cnt(N); // `cnt[u]` is the number of times we've visted node `u` in the current path
int ans = 0;
function<void(int, int, int)> dfs = [&](int u, int val, int time) {
if (cnt[u] == 0) val += V[u];
cnt[u]++;
if (u == 0) ans = max(ans, val); // Only update answer if the current node is `0`.
for (auto &[v, c] : G[u]) {
if (time + c + dist[v] > maxTime) continue; // if the current time + the edge time + dist[u] is greater than maxTime, skip
dfs(v, val, time + c);
}
cnt[u]--;
};
dfs(0, 0, 0);
return ans;
}
};